Introduction
To first order, is there a weight advantage that accrues from having more or fewer cylinders. That is, which is lighter for a given displacement, a single cylinder engine or one with many cylinders? I will show that, to first order:

The proof of this is as follows. Consider a single cylinder "square" engine, that is, one in which bore equals stroke. To start with, we will compute the mass of the cylinders as the number of cylinders increases. If we subtract a solid geometric cylinder from a cube we have the following shape:

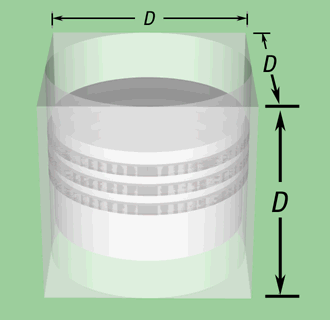
IF WE DEFINE:

m_n = mass of the cylinders for an engine block with n cylinders
d_n = diameter of all cylinders in an engine block with n cylinders
n = the cylinder count, i.e. the number of cylinders in the engine

AND

If we assume that:

The material of the engine block is of uniform density, then mass is directly proportional to volume.
The circular cylinders are idealized to be the full width of the block.

Regardless of the tiling used to arrange the cylinders with respect to each other,

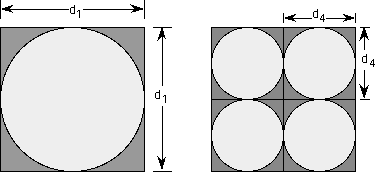
(An astonishing thing about this diagram is that if we use surface area as analagous to volume and perimiter as analagous to surface area, that four these circular figures, the "volume" remains constant but the surface area doubles. This fascinating result is why losses grow with n but mass does not…)

the mass of the engine cylinders resulting from the Boolean subtraction defined above is given by the expression:

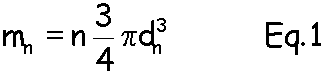
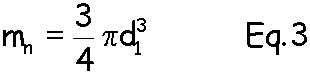
Since d₁ is the fixed displacement of the engine, Equation 3 states that the mass of the cylinder heads do not change as a function of n. Therefore we have proved the assertion that to first order,

A similar argument can be made for the pistons modeled as geometric cylinders of fractional engine block height. The results are the same and the relation obtained varies only by a constant. -LVW