Differential Protein Survey of a Breast Cancer Tumor

Differential Protein Survey of a Breast Cancer Tumor
- A Computational Oncology Project
L. Van Warren
Warren Design Vision
Experiment Design: Part One

I propose the following thought experiment. Differentiate the proteins that occur in normal tissue from the proteins that occur in tumor tissue derived from the same normal tissue type. This project seeks to understand first the number, then the type, and ultimately the function of proteins that are unique to the tumor and those that are unique to the normal tissue. To begin our line of reasoning, proteins that occur in the normal tissue are placed in a list labeled A. Proteins that occur in the tumor tissue are members of a list named B:

A	B
Normal Cell DNA/RNA	Tumor Cell DNA/RNA

The goal is to discover and compare those proteins that are unique to each list and the relative quantities of their expression. DNA contains the manufacturing keys to protein synthesis. It is sought to recursively subdivide both normal and tumor DNA, using restriction enzymes, eliminating identical parts of the DNA apparatus to reduce the scope of the search to just those proteins that differ between lists A and B. Divide and conquer is a commonly applied computational technique, where a large problem is divided into multiple smaller problems, for example list sorting as in qsort. These smaller problems are then themselves attacked by the same divide and conquer technique until a special termination condition is reached. This paper proposes to apply divide and conquer, not to the problem of sorting the lists, but rather to the problem of identifying those sections that are different in the Normal and Tumor DNA.

The terminating step of the divide and conquer algorithm is:
a) that point at which protein synthesis is disabled by the technique. OR
b) the point at which the Normal DNA and Tumor DNA are determined to be identical.

Every cell requires growth signaling. Broken growth signaling may occur, not as the Boolean of an OFF or ON, but rather as the Continuous or Intermittent Over or Under expression of a signaling substance. If this is the case then n, the number of proteins made by normal DNA will equal m, the number of proteins made by tumor DNA and a Boolean approach will fail. Further the entries in each list will be identical. If unique proteins arise, such as in myeloma this is ideal since we would like to associate particular substances with the pathological state.

Protein Arity: Three Possible Outcomes

#	Case	Normal Cells Synthesize:
1)	n < m	fewer proteins than tumor cells
2)	n = m	the same proteins as tumor cells
3)	n > m	more proteins than tumor cells

Remarks:
Discovering the SAME NUMBER of proteins in cases A and B does not mean that the SAME proteins are present. This observation also applies in the n < m, and n > m, cases.

Example: Same Number Does Not Mean Same Proteins

1.1)	Normal cell type A could produce two proteins called {a, c}
1.2)	Tumor cell type B could produce two proteins called {c, d}

Protein count is the same, protein type is not.

Suggestions:
It was suggested by Nair that this differential comparison approach could be extended to intracellular, extracellular and cell membrane proteins.

It was suggested to Munshi that PCR/cDNA amplification could be used to recover the genetic machinery that gave rise to the proteins. This would salvage a particular sample I had hoped to tissue culture but was damaged by freezing.

Note that this work does not attempt to map parts of the normal tissue gene that may carry defects in tumor suppressor genes such as BRCA1. Rather the purpose here is to compare tumor DNA and normal DNA with the sole intention of differentiating tumor protein synthesis and expression from normal tissue protein synthesis and expression.

Microdissection:
It was implied to me by Munshi that microdissection of the sample would decrease the likelihood of cross contamination. UAMS has recently acquired a confocal microscope that could be helpful to this end. For example. If normal tissue DNA was found to be mixed with the tumor tissue DNA, then both types of DNA would be amplified. Contrawise if tumor tissue DNA contaminated the normal tissue DNA then again both types of DNA would be amplified. I will prove below that one sided contamination from either side is allowable, but two sided cross contamination is not.

Contamination:
There are three contamination cases. The term one-sided contamination indicates that A has traces of B, but B does not have any trace of A. The same remark applies if we switch the roles of A and B. First a quick review of Boolean algebra.

Boolean Algebra:
There are three fundamental operators in Boolean algebra, AND, OR & NOT:

Operation	Word	Symbol	Example	Meaning
set intersection	AND	&	A & B
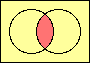set union	OR	\|	A \| B
set negation	NOT	^	^A
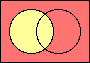set difference	MINUS	-	A - B

Notice that set difference is a derived operator, and can be expressed in terms of the three primitive operators. Back to our problem:

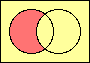Definitions:
A = List of Proteins Generated by Normal DNA
B = List of Proteins Generated by Tumor DNA
A' = (A | B) = List of Proteins Generated by Normal DNA contaminated with Tumor DNA)

Case 1: We will begin with the least likely case, one-sided contamination of A with B. Imagine that due to specimen contamination, we find ourselves in Case 3 of the protein arity table above. List A is contaminated to include List B as a subset. We call this contaminated list List A', the prime being the contamination operator. We seek to subtract List B from List A' to obtain a list of proteins that are only in the clear margin, i.e. the true List A. Or more succinctly:

Given A' and B recover A. Note that we may not know that A is contaminated! (As in the case where the tumor DNA is the DNA of normal tissue or self.)

A'
a b c d e f

B
d e f

A
a b c

We can perform an interesting quality control check.

A'
a b c d e f

A
a b c

B'
d e f

Note that if A' - A = 0 then A was uncontaminated and have obtained a positive result.
If A is the empty set then there is no tumor unique DNA.

Now having recovered the true A, we can compare this list with the true B and proceed.

Special Circumstances:
Two circumstances could bring us into the A = {a, b, c, d, e, f} and B = {d, e, f} case.
1) A was contaminated with B, meaning A is really A' OR
2) A, the Normal tissue makes three more proteins than B, tumor tissue.
We can't always determine which of the two special circumstances is in force. This will be termed aliasing.
Note also that we are now tacitly equating a tissue type with the proteins it produces, which if you think about it seems reasonable.

Case 2:
Imagine that we switch the roles of A and B, so that A is tumor protein list and B is normal protein list. We can now run through the same argument again. This is the second case, one sided contamination pointing the other direction. We get this work for free by switching the roles of normal tissue and tumor tissue. This is the more likely case, where we got clear surrounding margin tissue, but when sampling the tumor, some normal tissue was inadvertently included.

Case 3:
In this case both A and B are contaminated with each other to produce the lists A' and B'. Now we presumably cannot recover any proteins unique to A and B because the Boolean rules that governed the previous situation now have to be promoted to continuum rules where we talk about amounts of different proteins and begin to use words like under and overexpression of proteins. Differential amplification (making more tissue specific protein if more of a given tissue type is present in a mixed sample.) would also be useful if our Boolean thesis failed and we were in a pure under or overexpression situation, without the clear absence or presence of tumor specific proteins.

Conclusion:
With this reasoning in hand, the next step is to arrange for proper handling of the frozen tumor and normal material, microdissection and PCR amplification of the two tissue types.

Footnotes:
Lynn's breast cancer has been intervened aggressively by traditional methods of lumpectomy, axillary node dissection, chemotherapy (4 rounds of Adriamycin/Cyclophosphamide) and will soon be maintained via radiation and tamoxifen, an estrogen inhibitor. Her particular line of breast cancer was histologically characterized as aggressive ductile carcinoma and is hormone receptor positive, thus a good candidate for tamoxifen therapy. However, at the core of this illness is a genetic predisposition. For Lynn's progeny to be free from the curse of this disease, a genetic cure must be sought and understood.

There are three difficult problems that must be solved for Lynn to be healed of breast cancer in the most permanent sense:

The Mapping Problem

The Design Problem

The Inoculating Problem

PCR Kits - polymerase chain reaction
   AdvantageTM PCR Kits
   Panvera Long and Accurate (LA) PCR Kits
   Stratagene Product Highlights

References:
Adleman, Leonard M. Molecular Computation of Solutions to Combinatorial Problems, November 11, 1994 Science, (Vol. 266, page 1021)
DNA Based Computers, A Princeton University Survey on the World Wide Web
DNA Based Computers, Scientific American Q & A on the World Wide Web
Nair, Balan, MD. Hematology and Oncology Associates, private communication
Munshi, Nikhil, MD. UAMS Myeloma and Transplanation Research Center, private communication

Differential Protein Survey of a Breast Cancer Tumor
- A Computational Oncology Project
L. Van Warren
Warren Design Vision
Background Research: Part Two

Since this is a genetics project, some elementary genetics principles are in need of development. These are covered more thoroughly elsewhere. The definitions of DNA, RNA, the gene, the chromosome, transcription and coding are covered quite succinctly at The Human Genome Project.

It is also helpful to understand currently mapped landmarks of genetic origin that may apply to Lynn's specific cancer. These include BRACA1 & 2 (for which she has not been tested) and Her2Nu (for which she has been tested and is positive). I must confess at this writing my understanding on whether Her2Nu is a receptor issue or a genetic defect issue is lacking. It is helpful not only to understand these landmarks, but the process that gave rise to their discovery.

Sometimes it is helpful to consider unifying apparently different disciplines, for example the mapping of combinatorial problems onto genetic sequences could be combined with PCR amplification in a macro level process of resolve and amplify, resolve and amplify. In this case we can begin to think of PCR and combinatorial mapping as computational operators. Process design can then be thought of as mathematical equation construction, rearrangement, solution and optimization. We can work in symbol space when that is to our advantage, in numerical space and in reagent space in a manner that maximizes the contribution of each.

A helpful exercise along this line, is to consider classic sorting and search problems, embedded as sequence amplification, combination and rearrangement.