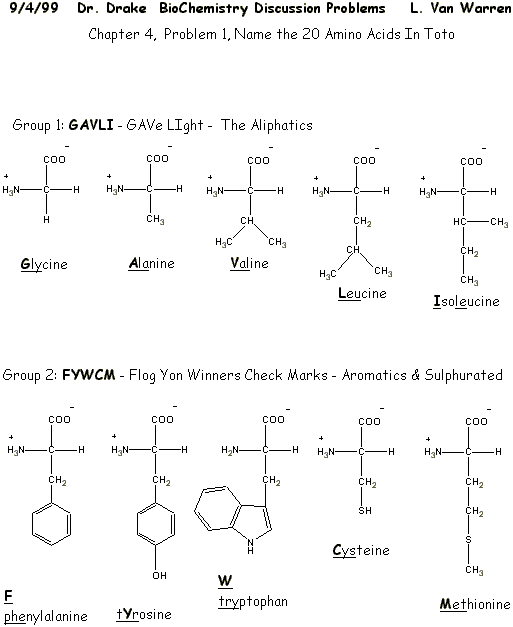
 |
 |
|
Dr. Drake
|
BioChemistry 5104
Problem Set 1 |
L. Van Warren
9/4/99 |
Chapter 3, Problem 4, part 1 states:
Q: It has been said that an army of dedicated monkeys, typing at random, would eventually produce all of Shakespeare’s works. How long, on average, would it take 1 million monkeys, each typing on a 46 key typewriter at the rate of 1 key per second to type the 18 character phrase, "to be or not to be"?
A: Let us begin by asking a simpler question. How long would it take 1 monkey typing at the rate of 1 key per second to type a specific letter?
Now as the monkey set about the task, he might hit the correct key on the first try. On the other hand, he might not hit the correct key until the last try. Let us assume that the average number of tries is the number of keys, 46, divided by 2. This yields 23 attempts on the average per correct character.
Now let us consider two key combinations. 23 attempts are required per character added to the string. So two characters requires, on the average, 23 x 23 key strokes. By induction we can see that a phrase n characters long would require:
timeToProduce(nCharacterString) = 23n [seconds]
If we put k monkeys to work we could cut the time down to:
timeToProduce(nCharacterString) = 23n/ k [s]
For the somewhat limited 18 character sonnet under the supervision of a million monkeys we have:
timeToProduce(18CharacterString) = 2318/ 106
[s] = 3.24 x 1018 [s] =
103 trillion years!
Note the bold text implies SUPERSCRIPTING.
Chapter 3, Problem 4, part 2 states:
Q: How long, on average, would it take one monkey to do so at a computer if the computer would only accept the correct letter in the phrase and then would shift to the next letter, that is, the computer knew what it wanted (i.e. a supervisor was present).
A: Now things aren’t as demanding for the monkey. We have a system that ignores noise and allows complexity to increase without combinatorial time penalty. The weakness is that we have been forced to introduce a "supervisory process" into the system to check the monkey’s work. Each 23 keystrokes on the average, the monkey adds one character to the string. Now the time complexity of sonnet production looks like:
timeToProduce(nCharacterString) = 23n [seconds]
For the 18 character sonnet under the produced of a single monkey and a good supervisor we have:
timeToProduce(18CharacterString) = 23n [s] = 23 x 18 [s] = 414
seconds
So the writing goes faster if Shakespeare is around.
Implications
By conjuring a smart supervisor, we sped the process up by eonic factors of time. To be intellectually honest, we must ask what the time and probability to form a smart supervisor is. If we assume that the supervisor has to only be as smart as a monkey then we can either put the supervisor monkey to work supervising, or assisting the other monkey in typing. The benefits of a supervisor monkey far outweigh the benefits of a typing monkey.
We have two options.
a) If the supervisor monkey is not as smart as the typing monkey then the supervisor monkey should by typing, not supervising.
b) If the supervisor monkey is exactly as smart as the typing monkey then why
can’t the typing monkey do better than random typing at constructing the string?
Deep Thought
If we assume that stellar systems condense from hydrogen gas to produce elements
heavy enough to make the likes of us, then the properties of living systems
manifest at higher levels of organization must be in some form driven by the
"wiring" or "rules" at the electronic and nuclear levels.
In a simple particle world, this means that nuclear binding rules and quantum
electrodynamic relationships that underly how aggregates of protons, neutrons,
and electrons behave are responsible for the form that we see life taking on.
 |
 |
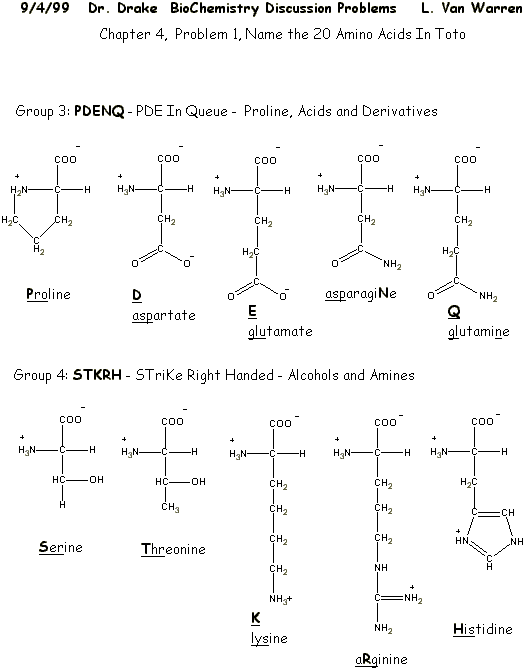
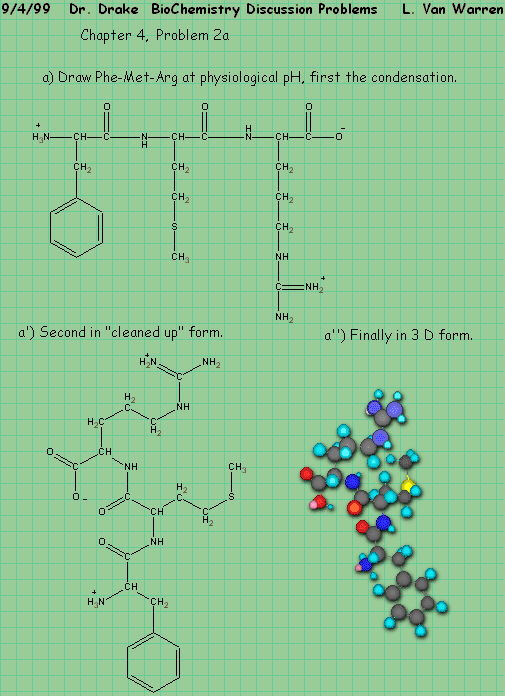 |
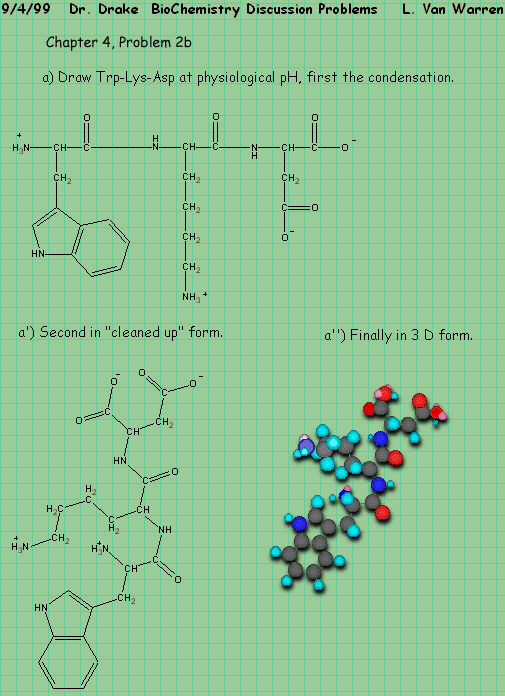 |
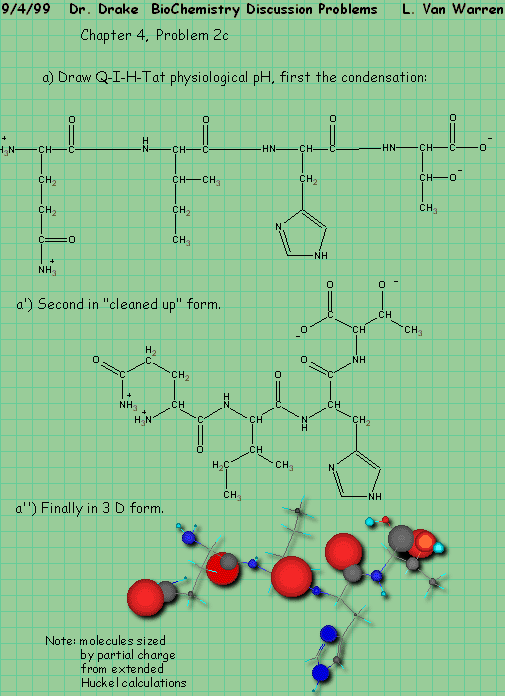 |
Chapter 4, Problem 3, states:
Q: How many different pentapeptides are there that contain one residue each of G D Y C L?
A: As in the case of the monkeys we will start by asking a simpler question,
How many dipeptides would there be, if there were only 4 amino acids?
By enumeration we have:
Aa, ab, ac, ad
Ba, bb, bc, bd
Ca, cb, cc, cd
Da, db, dc, dd
We note that the pattern is a square, that the number of entries in each row are four and that inverted patterns form as well as forward patterns. We notice that the forward patterns are in the upper triangle and vica versa in the lower triangle. Structurally the generating function is a square where each row and column have the four symbols as their headers. So we have in this trivial case: 42 dipeptides in our limited alphabet. But the problem excludes the repeated peptide case, so we are forced to strike the diagonal. Therefore the correct answer is 42 – 4 – 12.
The actual number of dipeptides is 202 or 400, but again we must strike the diagonal to produce 400 – 20 = 380.
In general we can extend our notion to a three dimensional cube for tripeptides to obtain the result for the question how many tripeptides?
The number of tripeptides is 203 or 8000. But the notion of striking duplicates from the hyperdiagonals must generalize to the higher dimensional spaces of the table. The corrected answer is 203 – 202 – 201= 8000 – 400 - 20 = 7580.
The general form is
NumberOfCombinations =
alphabetSizestringLength - alphabetSizestringLength-1.- … - alphabetSize1
Thus the requested number of pentapeptides is:
205 or 3,200,000 maximum possible number
- 204 or 160,000 those that repeat 5 symbols
- 203 or 8,000 those that repeat 4 symbols
- 202 or 400 those that repeat 3 symbols
- 201 or 20 those that repeat 1 symbols
= 3031580
So we see that the expressive power of the peptide language grows combinatorially
with string length.
 |
Chapter 6, Problem 6, part 1 states:
Q: A polypeptide is subjected to the following degradative techniques resulting in polypeptide fragments with the indicated amino acid sequences. What is the amino acid sequence of the entire peptide?
A: After transcribing the problem and carefully substituting the one letter abbreviations, we will work using a hand technique with paper and pen, then we will apply a slightly more automated approach that would be suitable for larger problems.
The first thing we do is refer to the Cyanogen bromide (CNBr) and Trypsin hydrolysis treatments themselves and ask the questions:
If the answer to 1) is no and the answer to 2) is yes, then we can treat this as a purely symbolic string matching problem.
Referring to page 114 of Voet&Voet, a luxury we may not have during an exam, we note that the peptide is probably less than 40 residues long and is eligible for direct sequencing.
On page 115 we note the remark that Cyanogen bromide cleaves on the C-side of Met residues. This leads to the critical constraint that
"any CNBr fragment that does not end in Met (M) must be terminal."
A similar constraint applies to trypsin digestion (hydrolysis)
"any trypsin fragment that does not end in Arg (R) or Lys (K) must be terminal"
We also note that trypsin has a slight limitation in that it will not cleave on the C side of Arg or Lys if the next peptide is a Proline. An observation to worth noting is that it is a little faster to line up the peptides first, and then apply these two constraints in a check pass. We assume that the authors have presented the fragments in N to C order, which is the convention for ordering peptide fragments. As such we proceed first by hand with a small puzzle:
In the first pass, we will establish the longest and most certain overlaps.
We note that string 3 and string 7 share the 3 letter sequence FAM.
They are combined and the list is updated:
In the second step, we note that string 1 and string 5 share the 3 letter sequence DIK. They are combined and the list is updated:
There are no more overlapping 3 letter sequences. We now proceed to note that string 2 and string 4 share the trivial 2 letter overlap YR. The update is:
Now string 3 and 5 share the 2 letter overlap QM. The update is:
At this point we make the note for possible future automation that the list shrinks from the top and lengthens towards the end. This has memory savings implications in a properly implemented memory management scheme that would allow us to sequence longer proteins in smaller amounts of RAM, an important detail for embedded computing applications. We now note the 2 letter overlap GM from strings 2 and 4. The update is:
At this point we can almost the sequence on a flimsy one letter overlap of K between strings 2 and 3. We also append the terminal K to obtain
Da dah!
In the second part of the answer, we will use the computer and a sliding window to make the solving of this puzzle easier. Unlike our reductionist strategy with pencil and paper, we sort the fragments into bins such that their overlap is maximized. Microsoft Excel was used to produce these tables, and I despair that it is not available for use during the exam as it is part of my forebrain now! Forging on nonetheless we have:
|
Initial State |
||||||||||||||
|
1 |
D |
I |
K |
Q |
M |
|||||||||
|
2 |
K |
|||||||||||||
|
3 |
K |
F |
A |
M |
||||||||||
|
4 |
Y |
R |
G |
M |
||||||||||
|
5 |
Q |
M |
K |
|||||||||||
|
6 |
G |
M |
D |
I |
K |
|||||||||
|
7 |
F |
A |
M |
K |
||||||||||
|
8 |
Y |
R |
||||||||||||
|
Final State |
||||||||||||||
|
1 |
D |
I |
K |
Q |
M |
|||||||||
|
2 |
K |
|||||||||||||
|
3 |
K |
F |
A |
M |
||||||||||
|
4 |
Y |
R |
G |
M |
||||||||||
|
5 |
Q |
M |
K |
|||||||||||
|
6 |
G |
M |
D |
I |
K |
|||||||||
|
7 |
F |
A |
M |
K |
||||||||||
|
8 |
Y |
R |
||||||||||||
|
Result |
Y |
R |
G |
M |
D |
I |
K |
Q |
M |
K |
F |
A |
M |
K |
Notes:
Chapter 8, Problem 1 states:
Q: How long should it take the polypeptide backbone of a 6-residue folding nucleus to explore all its possible conformations?
Repeat the calculation for 10-, 15-, and 20-residue folding nuclei.
Explain why folding nuclei are thought to be no larger than 15 residues?
|
Case 1: Assumption of Sequential Folding |
|||||||||||
|
n |
time |
||||||||||
|
(2) |
(n) |
bases |
6 |
5.3E-08 |
53 |
nanoseconds |
|||||
|
3 |
10 |
3.5E-04 |
349 |
microseconds |
|||||||
|
13 |
15 |
2.1E+01 |
21 |
seconds |
|||||||
|
10 |
20 |
1.2E+06 |
14 |
days |
|||||||
|
Case 2: Assumption of Concurrent Folding |
|||||||||||
|
n |
time |
||||||||||
|
(2) |
(n) |
bases |
6 |
1.1E-08 |
11 |
nanoseconds |
|||||
|
3 |
10 |
3.9E-05 |
39 |
microseconds |
|||||||
|
13 |
15 |
1.5E+00 |
1.5 |
seconds |
|||||||
|
(n-1) |
10 |
20 |
6.4E+04 |
0.7 |
days |
||||||
So the time constants of folding nuclei are such that n > 15 are not consistent with life in the time frames that we might expect to experience. It is interesting to note that allowing for concurrent folding changes the result by an order of magnitude, but probably does not allow for more than n > 16.
Chapter 8, Problem 4 states:
Q: Why are Beta sheets more commonly found in the hydrophobic interiors of proteins rather than on their surfaces so as to be in contact with the aqueous solvent?
Candidate reasons are compactness, Beta sheets are one of two compact conformations that protein polymers will tend to assume under hydrophobic forces. This compactness could conceivably be seen to as a way of them minimizing their potential energy with respect to the aqueous solvent.
Another candidate reason could be mobility. Proteins tend to be mobile at their extrema and more rigid within their interiors.
Actually I find it surprising that beta sheets would be more commonly found in the hydrophobic interiors, since adjacent beta sheets are stabilized by hydrogen bonds, bonds that would seem to be more prevalent in an ionic media.
Chapter 8, Problem 5 states:
Q: Explain why Proline residues can occupy the N-terminal turn of an alpha helix?
Because conditions are sterically favorable. Proline does not participate in hydrogen bonding.