Factoring Proteins

Factoring

Sequences

Van Warren

Warren Design Vision

1996

Introduction

Proteins, the building blocks of life, can be represented as sequences of consecutive symbols. At a primitive level, the four nucleic acids represented by C, T, A and G code for a set of twenty primitives, the amino acids. The amino acidsare assembled into substructures with identifiable functional roles.

The goal of this note is to apply the concept of substructures - repeatable patterns and subunits - in an indirect way. Instead of attempting to deduce the function of substructures directly, this work seeks to catalog them by progressive abbreviation; To identify the frequency of occurrence of constituent fragments which are present in various proteins, enzymes, viruses, and genes. It is hoped that an indirect approach of this sort might lead to some insight about higher level function.

By identifying and counting repeating substructures it is hoped that some sort of a clue, some tiny insight might appear, which would yield value to an experienced worker, who would perhaps be able to deduce the role of that more complex assemblage. I got this idea from my work in finite element modeling where simple structures are repeatedly assembled into larger ones with more complex roles.

Questions

We take as a working example a ribosomal protein that plays a role in breast cancer, L-19. We begin by asking some statistical questions about L19:

1) What is the longest substring in L-19 that repeats? Call this substring S1.

2) How many instances of this substring are there? Call this count C1.

We continue by asking this question again in successively smaller increments, to wit:

3) What is the next longest substring in L-19 after S1? Call this substring S2.

4) How many instances of this substring are there? Call this count C2.

The telecommuting pioneer, Herb Younger of JPL once said, "When all you have is a hammer, everything looks like a nail." Applying his maxim we obtain:

5) What is the incidence of successively smaller substrings in L-19? We will number these substrings S3 - SN.

6) What frequency of incidence can we associate with substrings S3 - SN? Call this C3 - CN.

Answering these questions enables us to produce a table of all repeating substrings together with a frequency of each. Possessing this table would allow us to surmise what fraction of L-19 consists of things that repeat, and what fraction consists of things that are unique, thus this technique's name. On viewing this table, perhaps one might deduce some fact relating to substructure function, some kind of clue relating to purpose, simply by viewing the extent of repetition of various primitive substructure patterns at consectutively higher levels of organization;

Combinatorial Analysis

Before we go about answering the six questions above, we need to do some analysis. To "count the cost" prior to embarking on an experiment, we need to calculate how much computer memory and running time will be required to complete the operation for a given sequence. In computer science parlance this is called, "finding the space and time complexity" for the method.

First we observe that for a string S0 of arbitrary length C0 there are:

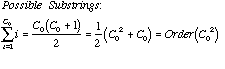
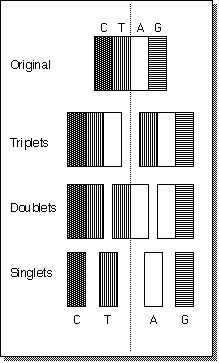
The term "Order" implies the rate at which the number of substrings grows as a function of string length. In the above case we see that the growth is quadratic. This can be seen by looking at the diagram of a trivial case, the nine unique substrings of CTAG - the title figure of this article. Starting at the second row and working down we have 2 strings + 3 strings + 4 strings. We note that the total number of rows equals the length of the original string which is consistent with the summation expression given above.

Noting that we have cubic growth, we plot the expression and obtain the graph of space complexity:

Our analysis implies we must store all the substrings simultaneously. In fact we can generate them a row at a time, with a considerable savings of space. With a little cleverness we can make the storage requirement obey a linear growth law, meaning that there is a linear relationship between the length of the original input string and the storage required to generate the substrings. This is very desirable.

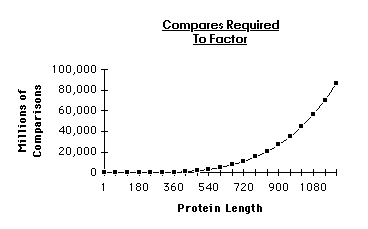
To obtain the execution time we must find the number of comparisons required. To do this we compute the number of comparisons performed on each row with the understanding that we compare all substrings on a given row with each other to find repeating occurrences.

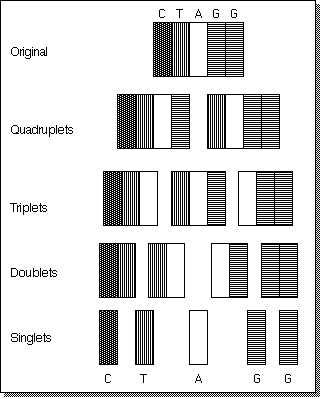
The figure above shows how a more complex string (chosen arbitrarily) would be broken into its possible substrings. The execution time complexity is the sum of the product of the comparisons per row and the length of the strings in that row:

More precisely we have:

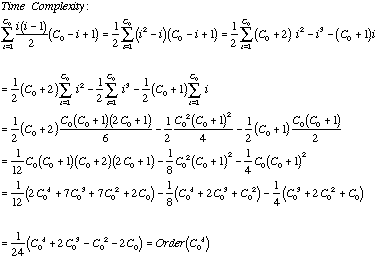
Plotting the time complexity we have:

facString Usage and Development

A 'C' program which implements this factoring algorithm was implemented. It reads the sequence of interest, factors it and prints the results.

Its usage is as follows:

facString sequenceFile

Sequence File Format:

sequence_length longest shortest

sequence

where:

sequence_length : an integer specifying the length of the sequence.

longest : the length of the longest repeating string to search for.

shortest: the length of the shortest repeating string to search for.

sequence: any sequence of letters representing nucleic or amino acids.

For an exhaustive search one would specify longest as (sequence_length - 1) and shortest as 1. It is often convenient to bracket the search by setting these to a narrower range of more specific values. This saves computer time. A consequence of the way facString is implemented is that if longest and shortest are both set to 1, facString just counts c, t's, a's and g's,

A couple of interesting facts emerged during the writing of facString; It is not necessary to make copies or subcopies of the original string in order to factor it; Further it is not necessary to declare a specific set of symbols as significant, that is what we're trying to find. For convenience the input is limited to upper and lowercase letters so that numbers can be used for annotation. Substrings are represented as a pair of integer coordinates indicating positional station along the string. The output is annotated to show:

1) the origin of the first occurrence of a repeating sequence and

2) the distance away that successive instances were found.

An advantage of knowing the distance is that it is then easy to determine at a glance whether a repeating unit occurs as part of the current unit (a negative distance), whether it abuts directly with the current string ( a zero distance), or whether it occurs further away ( a positive distance). This is illustrated below. These distances can then be plotted. As mentioned above the implementation makes it fast to search for repeaters of a specific length. It is handy (as in fun) to run facString and then read the output file into Microsoft Excel for subsequent analysis.

Output Format

The short string output format is:

string number_of_reps (first _location) first_distance sec_distance ...

This is depicted below.

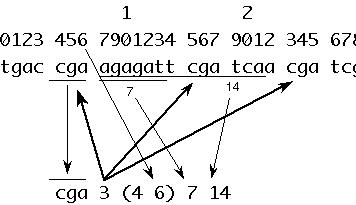
The long string output format is identical except that the string itself is not printed:

number_of_reps (first _location) first_distance sec_distance ...

This is easier to understand with an actual example. Recall that negative distance implies that the repeating substructure overlaps with its first instance.

A Test Example

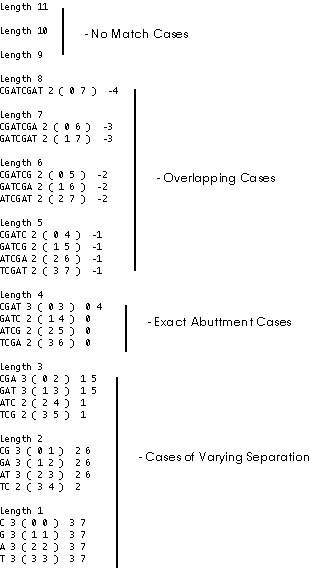
We will continue by factoring a sequence consisting of three repetitions of CTAG; CGATCGATCGAT is factored and those strings that occur more than once are printed.

testSequence statistics:

Stringlength: 12

Repeating Substrings: 62

Longest repeating substring(s):

Length 8: CGATCGAT 2 ( 0 7 ) -4

Longest repeating substring with no overlap:

Length 4: CGAT 3 ( 0 3 ) 0 4

Longest repeating substring with most repetitions, no overlap:

Length 4: CGAT 3 ( 0 3 ) 0 4

testSequence output:

With tested code it is now possible to answer the questions posed at the beginning.

Factoring L-19

L-19 was short enough to serve as a test and seemed to have relevance in the real world. Brookhaven and the National Institutes of Health maintain sequence data banks that one can access on the internet. I did so. The original annotated internet version of L-19 is included in Appendix A.

Input L-19

690 689 1

1 gggccgcagc catgagtatg ctcaggcttc agaagaggct cgcctctagt gtcctccgct

61 gtggcaagaa gaaggtctgg ttagacccca atgagaccaa tgaaatcgcc aatgccaact

121 cccgtcagca gatccggaag ctcatcaaag atgggctgat catccgcaag cctgtgacgg

181 tccattcccg ggctcgatgc cggaaaaaca ccttggcccg ccggaagggc aggcacatgg

241 gcataggtaa gcggaagggt acagccaatg cccgaatgcc agagaaggtc acatggatga

301 ggagaatgag gattttgcgc cggctgctca gaagataccg tgaatctaag aagatcgatc

361 gccacatgta tcacagcctg tacctgaagg tgaaggggaa tgtgttcaaa aacaagcgga

421 ttctcatgga acacatccac aagctgaagg cagacaaggc ccgcaagaag ctcctggctg

481 accaggctga ggcccgcagg tctaagacca aggaagcacg caagcgccgt gaagagcgcc

541 tccaggccaa gaaggaggag atcatcaaga ctttatccaa ggaggaagag accaagaaat

601 aaaacctccc actttgtctg tacatactgg cctctgtgat tacatagatc agccattaaa

661 ataaaacaag ccttaaaaaa aaaaaaaacc

Factored L-19 Statistics

Stringlength: 690

Repeating Substrings: 3545

Longest repeating substring(s):

Length 13 aaaaaaaaaaaaa 2 ( 674 686 ) -12

Longest repeating substring(s) with no overlap:

Length 9

gccaatgcc 2 ( 107 115 ) 147

aaaacaagc 2 ( 408 416 ) 245

aggcccgca 2 ( 456 464 ) 24

aaataaaac 2 ( 596 604 ) 53

Longest repeating substring with most repetitions, no overlap:

Length 7

caagaag 3 ( 64 70 ) 392 476

agaccaa 3 ( 93 99 ) 404 488

ggcccgc 3 ( 214 220 ) 236 269

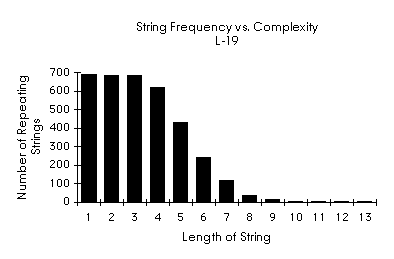
L-19 Observations

The longest repeating subunit with no overlap was 9 units long. This did not confirm the occurrence of repeating "micromachine" units I had hoped to find. This test did not take aliasing or wobble into account. Wobble allows for the substitution of various nucleic acids without changing the identity of the amino acid. Perhaps l-19 it is below the threshold of interesting substructures. An informative graph is :

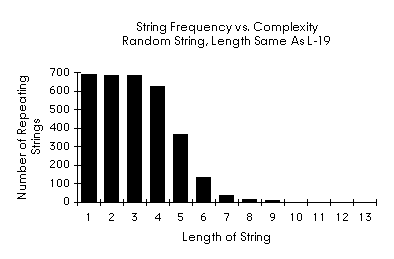
A Random Example

It appears that the histogram above does not vary markedly from that which would be produced by an arbitrary substrings. A computer science colleague, Rod Bogart, suggested that the digits of p might be an interesting place to look for "longest repeating substrings". Instead of looking at English text or the digits of p I generated a random string whose length was the same as L-19. The results are interesting:

Randomly Generated String 690 Statistics

Stringlength: 690

Repeating Substrings: 3260

Longest repeating substring(s):

Length 9

gtgggggtg 2 ( 61 69 ) 211

tccgttgcc 2 ( 367 375 ) 152

ttcagactg 2 ( 471 479 ) 18

Longest repeating substring(s) with no overlap:

Length 9

gtgggggtg 2 ( 61 69 ) 211

tccgttgcc 2 ( 367 375 ) 152

ttcagactg 2 ( 471 479 ) 18

Longest repeating substring with most repetitions, no overlap:

Length 7

gggggtg 3 ( 63 69 ) 213

ctcggtc 3 ( 91 97 ) 11

Random Observations

Surprisingly the randomly generated string shows organizational statistics that are strikingly similar in form to those of L-19. This tends, to a first approximation, to refute the presupposition that functions are organized by substructures of linear sequences.

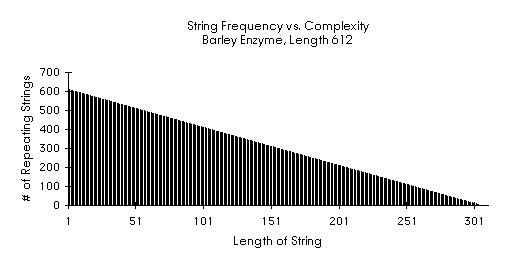
Factoring Barley Hydrolase 612

The protein databank version of Barley Hydrolase are included in Appendix B. This is a synthetic example since it is known that this material consists of two distinct fragments, however it proves that multiple instances of complex structures can be found via the facString program. Amino acids were encoded into single letters by arbitrary substitution. Program facString does not depend on the encoding.

Encoding of Barley Hydrolase 612

ILE: I, GLY: G, VAL: V, CYS: C, TYR: T,

LEU: L, PRO: P, SER:S, ARG:A, ASP: B,

GLN: N, LYS:Y, MET:M, PHE:H, ALA:D,

THR: R, TRP:E, GLU:U, HIS:J

Input Barley Hydrolase 612

612 310 1

IGVCTGVIGAALPSASBVVNLTASYGIAGMAITHDBGNDLSDLAASGIGL

ILBIGABNLDAIDDSRSADDSEVNAAVAPTTPDVAIYTIDDGAUVNGGDR

NSILPDMAALADDLSDDGLGDIYVSRSIAHBUVDASHPPSDGVHYADTMR

BVDALLDSRGDPLLDAVTPTHDTABAPGSISLATDRHNPGRRVABNAAGL

RTRSLHBDMVBDVTDDLUYDGDPDVYVVVSUSGEPSDGGHDDSDGADART

ANGLIAJVGGGRPYYAUDLURTIHDMHAUANYRGBDRUASHGLHAPBYSP

DTAINH

IGVCTGVIGAALPSASBVVNLTASYGIAGMAITHDBGNDLSDLAASGIGL

ILBIGABNLDAIDDSRSADDSEVNAAVAPTTPDVAIYTIDDGAUVNGGDR

NSILPDMAALADDLSDDGLGDIYVSRSIAHBUVDASHPPSDGVHYADTMR

BVDALLDSRGDPLLDAVTPTHDTABAPGSISLATDRHNPGRRVABNAAGL

RTRSLHBDMVBDVTDDLUYDGDPDVYVVVSUSGEPSDGGHDDSDGADART

ANGLIAJVGGGRPYYAUDLURTIHDMHAUANYRGBDRUASHGLHAPBYSP

DTAINH

Barley Hydrolase 612 Statistics

Stringlength: 612

Repeating Substrings: 93,942

Longest repeating substring(s):

Length 306

2 ( 0 305 ) 0

Longest repeating substring(s) with no overlap:

Length 305

2 (0 304) 1

2 (1 305) 1

Longest repeating substring with most repetitions, no overlap:

Length 7

4 (38 41): 70 302 376

4 (138 141): 92 302 398

Barley Hydrolase Observations

Besides the obvious fact that facString finds the two identical substructures, the most conspicuous feature is that the shape of the histogram is linear, not sigmoidal as in the two previous cases. This linear shape comes from the fact that a repeating pattern of significant length has been detected.

Conclusions

L-19 appears for all intents and purposes to be no more sophisticated than its randomly generated counterpart. Repeated idiomatic expressions are common in computer programs and various other coded language. We see no definite evidence of repeated idiomatic expressions in L-19 when compared with a random control. This is surprising. The Barley Hydrolase example confirms that high level structures of significant complexity can be found using the technique.

Future Work

Further work includes running this on wider variety of more sophisticated sequences . Coding by amino acid rather than by nucleic acid reduces computer time requirements and accounts for aliasing. It would interesting to look at other plants, microorganisms, enzymes and viruses. It would also be informative to look for aliasing at higher levels of organization.

Looking at how other coding systems embed information might be useful in some kind of "Comparative Coding" or anatomy of coding schemes.

Since this all looks like codebreaking, it might be interesting to combine the expertise and resources of the NSA with those of the NIH and let the big guns have at it. ·

Acknowledgments

I got this idea when I was visiting Steve Mittelstaedt who was doing some pipetting one day in his office at UAMS. I asked him what he was doing and he said, "Sequencing" with a mystique reminiscent of the word "Plastics" whispered in The Graduate. I had come to his lab get some liquid nitrogen, and while waiting I noticed a chart of amino acids on his wall. "Sequencing" kept ringing in my head, it seemed so similar to "Text Processing" which I had done for several years in a computer science context. A few days later his mother, Bo Mittelstaedt, was kind enough to answer some basic questions and helped me articulate the notion of factoring sequences like symbolic expressions.

Appendix A: Internet Posting of L-19

LOCUS S56985 690 bp mRNA PRI 07-MAY-1993

DEFINITION ribosomal protein L19 [human, breast cancer cell line, MCF-7, mRNA,

690 nt].

ACCESSION S56985

KEYWORDS .

SOURCE human MCF-7 breast cancer cell line.

ORGANISM Homo sapiens

Unclassified.

REFERENCE 1 (bases 1 to 690)

AUTHORS Henry,J.L., Coggin,D.L. and King,C.R.

TITLE High-level expression of the ribosomal protein L19 in human breast

tumors that overexpress erbB-2

JOURNAL Cancer Res. 53, 1403-1408 (1993)

STANDARD full automatic

COMMENT GenBank staff at the National Library of Medicine created this

entry [NCBI gibbsq 127871] from the original journal article.

This sequence comes from Fig. 2.

NCBI gi: 298485

FEATURES Location/Qualifiers

source 1..690

/organism="Homo sapiens"

/note="human"

CDS 12..602

/note="Method: conceptual translation supplied by author.

This sequence comes from Fig. 2. NCBI gi: 298486"

/codon_start=1

/product="ribosomal protein L19"

/translation="MSMLRLQKRLASSVLRCGKKKVWLDPNETNEIANANSRQQIRKL

IKDGLIIRKPVTVHSRARCRKNTLARRKGRHMGIGKRKGTANARMPEKVTWMRRMRIL

RRLLRRYRESKKIDRHMYHSLYLKVKGNVFKNKRILMEHIHKLKADKARKKLLADQAE

ARRSKTKEARKRREERLQAKKEEIIKTLSKEEETKK"

BASE COUNT 216 a 175 c 184 g 115 t

ORIGIN