Dear Brian -
This is the nonsequential notation I was telling you about. (Screen wide please). I am calling it thingRep™ to indicate that the expression represents a single complex entity. The first blue image shows the equivalence between a textual representation and a graph representation. The second image suggests what a very complex expression might look like and starts to look like a colony of cells. This suggests that cell colonization is a mathematical property driven by expressions written in the symbolic text of DNA. This equivalence idea occurred to me a couple of months ago when I was looking at the beatiful images on the Caida-Walrus web site. After you and I were talking about Riemann Conjecture, Zeta function and Goldbach I went on a bike ride in fast and busy lunchtime traffic. The kind where people don't care if you become roadkill. When I wasn't yelling at cars not to kill me, I got to thinking. I started to write a letter, but decided a picture was more succinct:
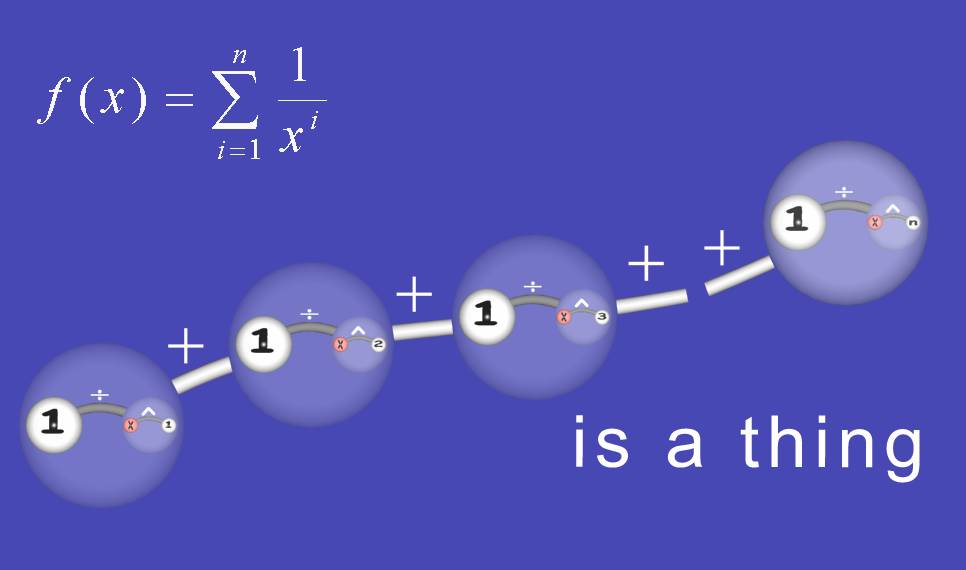
Consider the thingRep shape. You can grab it anywhere, and you can see it all at once and it has no beginning or end. Complex expressions would look like colonies of cells growing in fluted clusters.
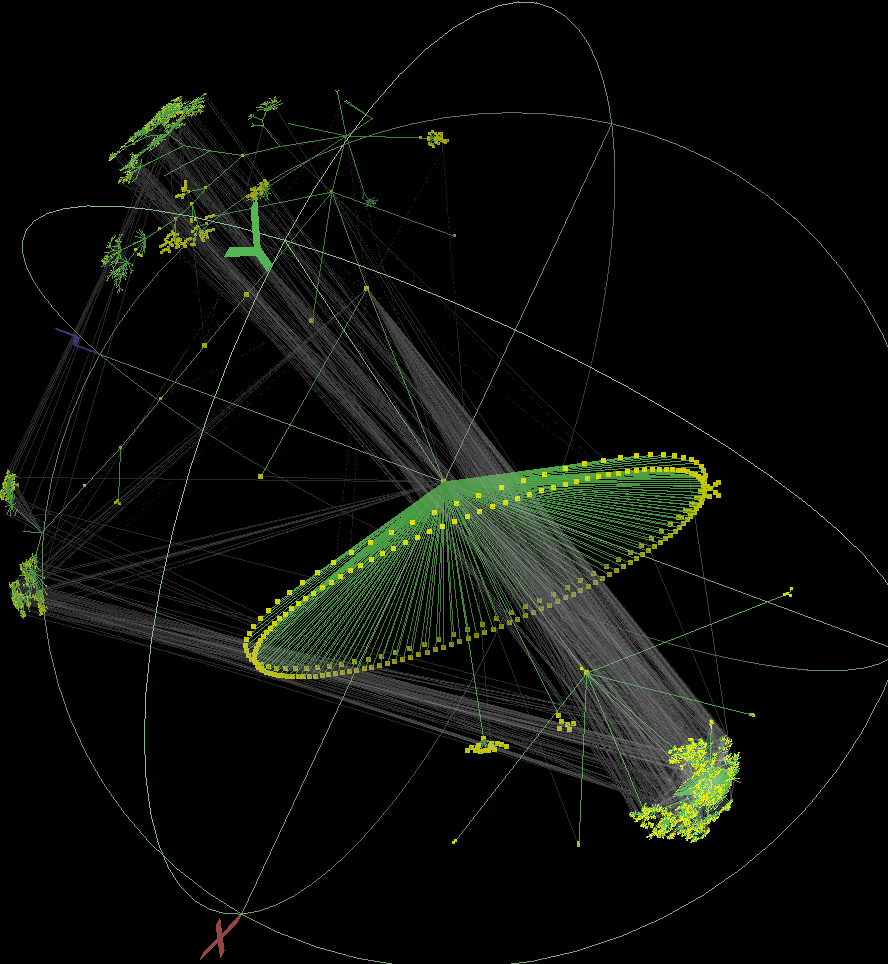 -- graphic courtesy
CAIDA project
-- graphic courtesy
CAIDA project
Colonies of cells can be reduced to complex expressions LIKE DNA SEQUENCE and binding protein state.
In traditional summation notation like:
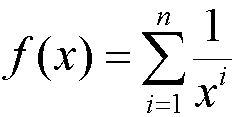
a subtle bit of tyranny has crept into our thinking. I call this, the curse of sequentiality and it is a perceptual, human factors, thinking compartment, psychophysical curse, much like that which occurs when you read each consecutive word in this uh sentence. A little noodle of brain cells commits to operating and thinking about the terms of this series one at a time, like a magician gets you to look at the card he wants you to see instead of the deck he is jacking up. See I am doing it right now.
ThingRep™ lets you see things as decks or as cards as you prefer, INSTANTLY with many parts of your brain.
Step 0) Write a good interactive graphics program for translating equations into thingRep™. See appendix.
Step 1) Get used to doing math in thingRep™, instead of symbolic rep. You’ve been down that road all your life, you know where it leads. All math gets done in thingRep from now on. Just accept it, like learning to use a new editor.
Yes it hurts, do it anyway.
This step is very important. This will be easier for kids who grow up in thingRep than us.
There are standard factorizations and regroupings that take place in thingRep that are very beautiful.
What I want to focus on today is that using shape to convey meaning instead of text allows a bunch of additional brain centers to get to come to the party. You can just see the solution instead of having to plod through it. If you want to do the really neat stuff, this is the only hope. thingRep delivers us from the curse of sequentiality. You see all the terms, not just some printing. Meta-instantiation is easier, errors are decreased. More horsepower baby.
Step 2) Rearticulate Fermat in thingRep.
Step 3) Rearticulate Riemann and Goldbach into thingRep™.
Step 4) Prove something.
Step 5) Go to Oslo.
Step 6) Die.
Dedicated to MIT's great Norbert Weiner who said, “What we need is not notations but notions”. He knew thingRep was out there. Thanks to CAIDA for the use of their graphic. Tara Munzner at UBC has written some cool 3D software that might make a good starting point.
- Van
L. Van Warren
Producer
CellWorld
501-224-7434 home office
501-231-5426
cell
www.wdv.com
Appendix – thingRep’s developer reference
1) Develop a thingRep interpreter, such that if you type in an expression, you get back a thingRep picture.
2) Develop a thingRep transfomer, such that If you type in an operation, you get back a thingRep animation.
It turns out that as you type the expression, it draws whatever thingRep it can for how much you gave it, like filec in csh.
You can replay the animation by moving the slider and saying, “oh”.
You can change the POV for each step in the animation so you can see the card or the deck.
3) Develop a thingRep inverter that does the opposite of 1) and 2). You must also be able to create a thingRep directly and then have it write down the symbolic expression. This inverse translation direction is very important for printing out results.
See knowledge mapping links for background.