Chapter 4: Ideal Filtering in the Frequency Domain
" Hey Man, Nice Shot" - Filter
Introduction
In this section, we will introduce filters. The basic idea of a filter is to allow certain frequencies
of a signal to pass through while blocking all others. A common example is the tuner on your
radio. The tuner rejects all the frequencies except those of the station you select. In times past,
this was done with analog circuits that resonated with the selected station's frequency band.
Now a new kind of radio is being done with digital signal processing. It is called soft radio, not
to be confused with easy listening or pirate radio. Now back to filtering.
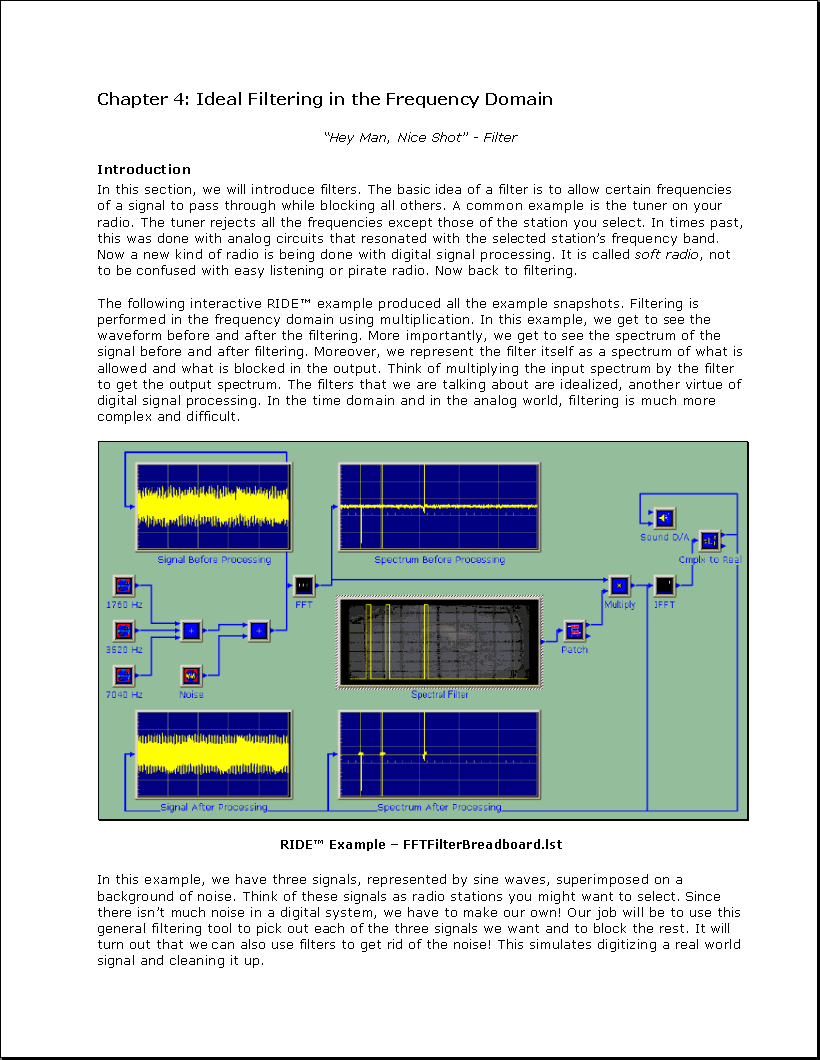
The following interactive RIDE(tm) example produced all the example snapshots. Filtering is
performed in the frequency domain using multiplication. In this example, we get to see the
waveform before and after the filtering. More importantly, we get to see the spectrum of the
signal before and after filtering. Moreover, we represent the filter itself as a spectrum of what is
allowed and what is blocked in the output. Think of multiplying the input spectrum by the filter
to get the output spectrum. The filters that we are talking about are idealized, another virtue of
digital signal processing. In the time domain and in the analog world, filtering is much more
complex and difficult.
RIDE(tm) Example - FFTFilterBreadboard.lst
In this example, we have three signals, represented by sine waves, superimposed on a
background of noise. Think of these signals as radio stations you might want to select. Since
there isn't much noise in a digital system, we have to make our own! Our job will be to use this
general filtering tool to pick out each of the three signals we want and to block the rest. It will
turn out that we can also use filters to get rid of the noise! This simulates digitizing a real world
signal and cleaning it up.