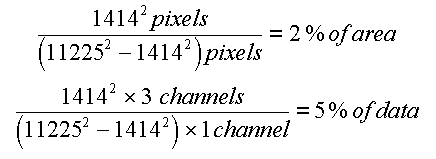• How Many Pixels Does an Eyeball Have?
• How many vision receptors are there?
• What is the spatial and temporal resolution of the eye?
• At what rate can the body express information to the outside world?

First Guess: The Eye has 90 Million "Pixels".
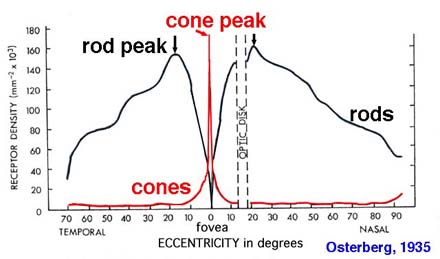
The figure above implies a reasonable value for optical receptor density is 100,000 receptors per square millimeter.  Retinal coverage of is nearly 180 degrees.  To compute the receptor count we need the diameter of the eye.  The radius of the average eye is 12 mm.  This implies that the surface area is 2 p r² or 904.7 square millimeters.  This first ordercalculation implies that average eye contains 90 million receptors. Most people have two. Eyes that is.  When building display devices, it is convenient to give pixels Cartesian (i, j) or (x, y) coordinates.  Based on this, if we were to build a display device that could simultaneously excite all the optical receptors, and if this display device  were a square, there would be 9512 pixels on an edge.

A Better Approximation: The Eye has 126 Million "Pixels"
According to Dr. John Penn, of the UAMS eye center, the adult retina has 126 million receptors.  He points out that not all of these are activated under all lighting conditions, to wit, "as light environment increases in luminance, rod response becomes saturated long before cones are maximally functional."

Washington neuroscience agrees with Dr. Penn.  According to this source there are 120 million rods and 6 million cones.
Using the figure of 126 million "pixels" or receptors a display device that met or exceeded the performance of a fixed, staring eye would have 11,225 pixels on an edge.

Only Cones See Color
An important detail in this pursuit is to notice that only the cone cells enable the perception of color. There are three kinds of cones, named the "red", "green" and "blue", designated L, M and S cones respectively.  Rods have a peak sensitivity in the green region of the spectrum at 500 nm.  Perhaps that is why night vision goggles use green as their luminance display color.  The cones, though concentrated in the central (foveal) region of the eye, are also distributed throughout the retina, but in low concentration relative to rods.  Rods take more time to acquire signal than do cones, up to 1/10 of a second.  Thus it is the peripheral cones that contribute to motion sensing, not the rods!  If you don't believe this, try playing tennis at twilight.  Your night vision won't do the motion processing job.  In exchange for their slowness the rods contribute extraordinary luminance sensitivity, down to a single photon.  There are 6 million cones.  Let us assume that there is an equal distribution of L, M and S cones.  Now define a  {red, green, blue} triple of cones as equivalent to a single pixel.  This yields two million "color" receptors that our display device must service, for a fixed and staring eye.  This corresponds to a square with 1414 pixels on an edge.

There Is No Fixed and Staring Eye
The only fixed and staring eye is on a dead person!  The living eye is constantly in motion, it must be or the image will wash out.  Books, television, movies and computer displays all require the eye to scan to new content rapidly both spatially and temporally.  These media are all fixed with respect to the coordinate system of an unmoving head.  We can now refine our display device calculation based on this.  If there was such a thing as a fixed and staring eye, then we could simply build a 1414 x 1414 color display and that would keep the fovea busy.  To occupy the rods this display would have to  sit in the center of a much larger 11225 x 11225 pixel display. This outer display would be gray scale only - or "green scale" as the case might be.  The inner display would have two percent of the area and carry five percent of the data of the outer:

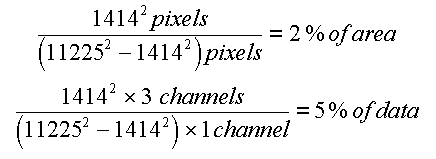
But this is only for a fixed staring eye.  If the eye moves to an adjacent point on the screen, it would be necessary for that part of the screen to become color and the rest to revert to the "gray".  Reliably tracking random eye movements and displaying the corresponding color/gray image is a formidable task.  Even if this could be done, it would not account for head movement.  Another alternative would be to put the display on or near the eye itself.

Spatial Resolution of Wearable and Static Displays
For a wearable computer the above arguments tells us that 1414² resolution foveal display at the six o'clock position of standard eyeglasses should be sufficient.  Once could, "draw the curtains" and go into work mode by supplementing with the high bandwidth peripheral display.  For safety reasons while walking on the sidewalk, only the foveal display would remain activated.  A tabletop, wall, television, movie or entertainment display that allows for eye movement, head movement and peripheral vision and  should accommodate the full resolution of the eye, in color!  We also want to acknowledge the architectural simplicity that results from choosing an edge dimension for the image that is a power of two.  If we choose 2¹⁴ or 16384 pixels on an edge as the figure that meets visual system performance then each image contains 268 million pixels.  Now we can move our eyes and turn our heads just like real people. For static displays he nearest power of two that meets or exceed the 11225 value is 16384 pixels on an edge.

Color Resolution
It is known that eight bits of intensity is unsatisfactory for color reproduction, particularly in the low blues, and that at least 12 bits are preferable. On computer architectures that align by the byte, a better size choice is 16 pits per color or alpha channel.    We have now defined spatial and color resolutions for static frames that meet computer architecture requirements and meet or exceed the visual system performance.  We have ignored the issue that most display devices cannot reproduce the dynamic range of intensities found in nature, however, 16 levels of intensity bring us closer.
If color pixels consists of four, sixteen bit words, our uncompressed image require 2.15 gigabytes of storage.  Armed with this design information, let us now define an idealized motion picture and transmission capability that would also be designed to the limits of the human visual system.

Temporal Resolution
It is known that many people are able to discern flashing at rates exceeding 60 Hz.  Fluorescent lights are a good example of this.  I can see the corners of this monitor flashing at 72 Hz.  It appears that cone vision is responsible for this temporal sensitivity.  If we were to make a choice that met or exceeded the performance of the human visual system, and was also a power of two, the nearest choice would be 128 Hz.  There is reason to believe that trained fighter pilots, baseball and table tennis players make motion decisions based on these kind of rates so this is entirely appropriate.

Content Channel Resolution
Having established that the user has two eyes, and needs to see imagery at 128 Hz, with 268 million pixels per image we now need to define the number of channels of content that might be made available to the user.  Convention cable systems have from 40 to over 100 channels.  Let us assume that 128 channels is sufficient to meet the needs of most content consumers at a level of quality that meets or exceeds the capabilities of the visual system.

We are not including the audio or haptic requirements of a sensory input limited system, but a similar calculation could be performed that utilized the touch sensor receptor density and  audio frequency range.  Haptic and audio bandwidth requirements are not nearly as severe as visual system demands.

A Calculation

Two Eyes x Channels x    Pixels/_Frame     x ^Bits/_Pixel   x ^Frames/_Sec
    2         x   128      x    268,435,456       x      64         x         128      =      6 x 10 ^{14 bits}/sec

   2¹       x     2⁷       x          2²⁸               x      2⁶         x         2⁷      =         2^{49  bits}/sec
 

So a system that met the performance requirements of the human visual system and satisfied the variety requirement of an intelligent user would require delivery devices and networks whose bandwidth is at least  600 teraHertz.
Such systems would have to operate on a wavelength shorter than 500 nanometers, which is in the range of green light.  To store a two hour movie at an appropriately sampled rate would require

2 x 1 x 268,435,456 x 64 x 128 x 3600 x 2 / 8 = 4 petaBytes (= 4000 Terabyte is 1000 Gigabytes)

This is a little more than a video tape currently holds!

Simplified Calculation for Monocular Displays
 
Traditional monocular displays include CRT monitors, liquid crystal displays, and projection screens that do not exploit polarized light. If we revise our estimates for current display technology and ask the question, "How much data can we deliver to the eye from a traditional display?", we have:

1 [Eye] x 1 [Channel] x 1024 x 768 [Pixels/Frame] x 4 [Bytes/Pixel] x 24 [Frame/Sec]

= 75 [Megabytes/Sec]

Gestural Bandwidth vs. Visual Bandwidth

We might compare this input bandwidth of the human being to the output bandwidth. Output bandwidth, or the rate at which we can express ourselves includes all vocalization and movement that could be digitally captured. This is a somewhat more difficult calculation but we can create an upper bound based on the number of joint degrees of freedom and the number of distinct positions, and the rate at which those positions could change.

Fingers have 3 degrees of freedom, 5 fingers gives 15 degrees of freedom (DOF). Fingers connect to wrist for 3 degrees of freedom, wrist to elbow 2 more, elbow to shoulder 3 more. So an arm has 23 DOF.

The torso, like the shoulder, has 3 gross DOF, dancers can add about another 6 fine DOF to that. The hips (we're wearing a body suit now) have 2, because it shares one with the torso. The legs are like the arms but the toes have 2 DOF. So a leg has 18 DOF.

The head/neck has 3 DOF (at least). We will leave the mouth alone, since it is used for talking, and the eyes alone since they are used for seeing, which we want to be independent of output. The forehead and cheeks have 3 DOF (at least).

A fully instrumented human has 23 + 23 + 3 + 2 + 18 + 18 + 6 = 93 degrees of freedom. Position can be encoded with varying accuracy depending on the joint. All positions can be mapped to a number space just like images are mapped to a pixel space. Motion, or change in position corresponds to animation of an image. If we assume 24 bits per degree of freedom, a complete position of the human body can be described by an image that is 10 x 10 pixels in size. The eye however can process color imagery 1400 x 1400 pixels in size. Thus the visual bandwidth of a person exceeds the gestural bandwidth by ~ 1 part in 20,000. Thus we collect information 20,000 times more effectively than we express it, if only gestures are considered.

What is the bandwidth of speech compared to gesture? There are two places to look, and three comparisons to make. One can compare the bandwidth of American Sign Language (AMSLAN) to speech. Speech is slightly faster. Experienced signers can almost keep up with careful speakers. Speech proceeds at 180 words per second, typewritten gesture is about a third of this figure.

Thus our ability to express ourselves exceeds the rate at which we can take information in by many orders of magnitude. This is important, and shows the prejudice imposed on us by the current generation of input devices. Perhaps the fastest way to help us communicate it to enable us to use gestures to make movies that express how we feel, and what we want to communicate.