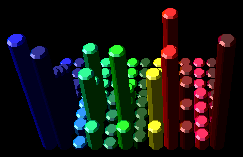
Introduction

The essential feature of using sound to drive computer animation is the transformation of a large number of Fast Fourier Transform (FFT) samples into a smaller number of animation controls, for example, the displacements of piano keys.

The overall scheme is:

1) Take sounds from the real world.

2) Perform an FFT to deduce the frequency components.

3) Use the frequency components as animation controls.

The first example of the use of this technique was the film, "Sound Into Graphics" by James Bozek, Patrick Kane and the author, presented at the 1984 SIGGRAPH computer graphics conference. For this project, frequency controls were used to modulate detailed motion, in this case, the motion of a set of prismatic keys with the fanciful title, "City of Keys". This accomplished the goal of a sound driven animation. Keyframe interpolation was used to control of the gross ensemble motion of the percolating City of Keys.

Overview

Typically, there are thousands of frequency components in the Fourier transform of a sampled sound, but there are only tens of controls that a user may desire to control an animation, morph, or transformation. As a specific example we will discuss the reduction of thousands of components to ninety-six for the namesake case of the City of Keys. The process is entitled, "Key Mapping".
A sound buffer is associated with each frame of film. These samples corresponding to the motion in that frame. For sound sampled at 40.0 kHz in a 30 Hz video soundtrack, we have:

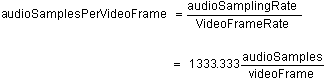
For each frame of the movie, we load a buffer with 1333± samples representing the intensity of the sound at those particular instants. There are two complications. The first complication is that we cannot load a fractional sample. The second complication is that the FFT requires us to use a buffer whose size is a power of two. Rounding up for the present example would require a 2048 element buffer. This buffer is passed to an FFT routine which does the classic computation and returns a buffer full of frequencies represented as complex numbers. For our purposes, here we will consider the power spectrum to be the square root of the sum of the squares of the real and imaginary components:

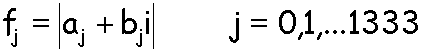
Frequency increases from left to right, with DC being sample zero and sample 1469 representing the highest frequency component available which according to Nyquist is half the sampling rate, 20 kHz in this example.

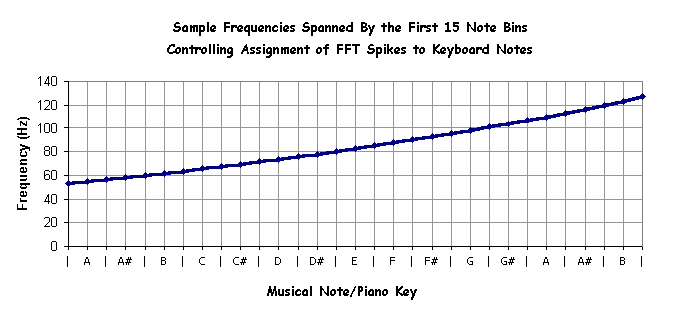
Definition: Each note on a piano scale represents a bin, into which we accumulate the frequencies.

The note spans all frequencies not subtended by its neighbors. This is illustrated above for the first 15 notes of the piano scale. Each octave in the musical scale represents a doubling of the frequency. The number of spikes available for accumulation into the note bins is therefore greater for high frequencies than for low. Plotting this for the whole audio spectrum yields:

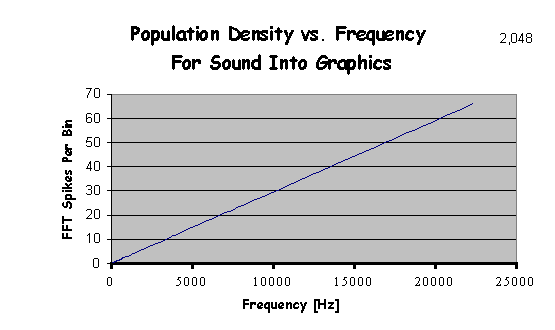
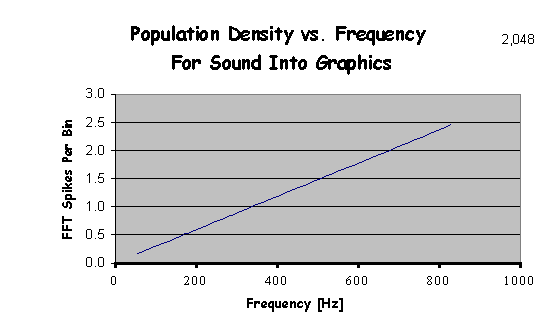
Performing FFT’s on each frames samples doesn’t yield a full spike to place in a note bin until we reach over 300 Hz, 349 Hz to be exact, two and one half octaves into the piano scale! The remedy for this is to increase the number of samples passed to the FFT. The question is how many samples do we need. ?" The answer turns out to be 16384 samples per FFT, and this number of samples is required whether we are sampling at 40 kHz as in the example above or at 44.1 kHz, the standard CD sampling rate. The next question is, "Well how many previous frames do we need? This number, 16384 samples, turns out to be 12.28 video frames of sound data at 40 kHz or 11.15 video frames of sound data at 44.1 kHz. It has been said that the FFT is not the best method for computing the power spectrum and here we can see why. For our application, we would prefer a method that does less work on the high frequencies and more on the lows, and returns magnitudes only, if doing so would be faster. Lacking a more convenient method, we press on.

Accumulation

With these definitions in hand we are now ready to describe the process by which samples are accumulated into the note bins, or alternatively control knob buffers for other applications. We start the process with a buffer organized as follows:

We assume each value in the FFT array to represent a magnitude of a given frequency occurring in our original sound signal. For purposes of computing accumulation, we will assume we are computing the area of those keys falling in the boundaries of a given note. To facilitate this integration we will assume each FFT spike is of unit width as in the diagram above.

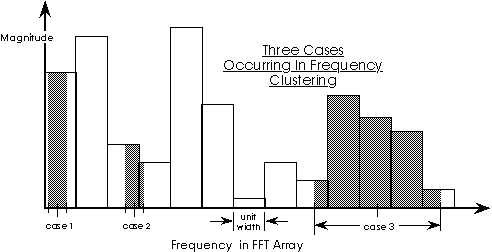
Three Cases

Three cases arise when performing this integration:

keyHeight: desired array of key heights for the City of Keys.

fftHeight: given array of fft results for a given frame.

note: given index of the musical note whose displacement is being sought assuming. This index varies from 0 for the a 55 Hz A, denoted by A0, and goes to 95 Hz for G# if we are processing eight octaves of material. (53 to 14493 Hz) tones ranging from 53 to 57 Hz are all assumed to belong to A0. Note that eight-octave processing does not use the audible frequencies from 14493 to 22050, but we do not exploit that here.

fftSpike: computed index into the fft array.
As shown in the diagram above there are fftSpikes for the left, cntr and rite coordinates of a note. For a given note, there are, within the space of these spikes, three floating point coordinates of interest. These corresponding to the frequencies at the left, center and right boundaries respectively, e.g. A0 center = 55 Hz. The routines for computing these are:

leftFreqOf(note):

Computes the frequency of the left boundary of the note, as a floating-point number.

cntrFreqOf(note):

Computes the frequency of the center of the note, as a floating point number.

riteFreqOf(note):

Computes the frequency of the rite boundary of the note, as a floating point number.
Corresponding to these three note coordinates are three possible FFT spikes.
Correspondingly there are:
leftSpikeOf(note):
   Computes the integer FFT index for the frequency of the left boundary of the note.
cntrSpikeOf(note):
   Computes the integer FFT index for the frequency of the center of the note.
riteSpikeOf(note):
   Computes the integer FFT index for the frequency of the rite boundary of the note.
Again, for eight octave work the notes are numbered from 0 to 95, with A0 = 55 Hz being the center of the first note.

leftSpikeBndy(fftSpike) returns the left boundary of the fftSpike, as a floating point number.

riteSpikeBndy(fftSpike) returns the left boundary of the fftSpike, as a floating point number.
We take the keyHeight for a given note to be the area under the discrete fft skyline. The area is computed as the sum of the individual areas (height times width), where the height is the value in the bin. The width includes the width of all bins subtended by a particular note, including fractional. It may seem strange to allow bins fractional width, but this is a common practice in the image processing context.

Case 1: Completely interior to a single FFT spike.

keyHeight[note] = fftHeight[cntrSpikeOf(note)] * (riteCoordOf(note)-leftCoordOf(note));

Case 2: A note spans two FFT spikes.

leftKeyHeight = fftHeight[leftSpikeOf(note)] *
(riteSpikeBndy(leftSpikeOf(note)) - leftFreqOf(note));
riteKeyHeight = fftHeight[riteSpikeOf(note)] *
(riteFreqOf(note) - leftSpikeBndy(riteSpikeOf(note)));
keyHeight[key] = leftKeyHeight + riteKeyHeight;

Case 3: A note spans more than two bins

leftKeyHeight = fftHeight[leftSpikeOf(note)] *
(riteSpikeBndy(leftSpikeOf(note)) - leftFreqOf(note));
middleKeyHeights = 0.0;
note = leftSpikeOf(note) + 1;

for(; note < riteSpikeOf(note); note++)
{
middleKeyHeights += fftHeight[cntrSpikeOf(note)];
}

riteKeyHeight =
fftHeight[riteSpikeOf(note)] *
(riteFreqOf(note) - leftSpikeBndy(riteSpikeOf(note)));
keyHeight[key] = leftKeyHeight + middleKeyHeights + riteKeyHeight;

Use

Once the 96 key heights are computed, these may be used as controls for animation.

© 1996-1998 L. Van Warren • Patrick E. Kane • All Rights Reserved