Second Generation
Biotechnology
Knowledge Mapping

L. Van Warren
Warren Design Vision
1/1/2001

The "prime directive" of knowledge mapping is to visualize cause and effect relationships at a large scale. Knowledge maps are the precursors to ontologies of biological pathways that include metabolism, signal transduction, gene transcription and protein translation. Pathways are the precursors to simulation and simulation is the precursor to predictive control and healing. First generation knowledge maps used the techniques described in the previous paper, but did not define how conditional facts should be handled in the fact extraction and knowledge mapping process. The purpose of this paper is to discuss and clarify the handling of conditional facts, also known as "predicates".

To describe this issue, a slight digression is necessary.

In theoretical computer science, you will hear statements like:

"a implies b"

"if a then b"

These are called predicates and they exert a relationship called implication which is written mathematically as:

a -> b

In a computer program written in an imperative language, such as Java or 'C', predicates are statements of the form:

if (expression₁) then { expression₂}

These kinds of statements also appear in applicative (AKA declarative) languages such as Lisp and Prolog with different syntax. These statements are adorned with various sorts of punctuation so that they can be scoped and parsed, then compiled or interpreted and then executed by the machine.

The expression₁ under the if is evaluated, and if it is true, then expression₂ is executed (or asserted), if expression₁ is false, execution "falls through" to the next statement without expression₂ being executed (or asserted).

In knowledge mapping, we extract facts from the literature that represent cause and effect relationships.  We model these relationships as expressions of the form:

a is related to b

or

"a" "is related to" "b"

which is graphed as:

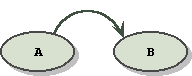
No arrow would appear in a commutative relationship, and the convention is that the doer points to the doee.

The graph can be represented symbolically as:

aRb

An expression of the form aRb is called a "fact". Facts that share common entities can be drawn into knowledge maps. Facts can be compounded as in the transitive case:

aRb and bSc implies aRbSc,

we can perform an abstraction step to obtain

aTc where T is the abstraction of the group RbS.

Conventions:

Lower case letters, {a, b, c} represent entities, objects or noun phrases and
upper case letters, {R, S, T} represent relationships between entities.
Relationships appear in English as verb and prepositional phrases.
Entities, objects, substances and things appear as noun phrases.
Nouns should not appear in verb phrases, and vica versa, though because of the frailties of English, nouning a verb and verbing a noun often happen and must be dealt with.

When translating English journal text into sets of cause and effect relationships, facts sometimes appear that do not properly fit into the framework of aRb because they are dependent on some condition that is external to aRb .  In other words they are conditional facts, that is, facts that are only facts if some other condition is satisfied.    Consider the following text, in a paper on proteins in growth and signaling pathways important to understanding cancer. It is not necessary to understand protein chemistry in order to consider the following example:

On recruitment of Sos to the cell membrane, Sos binds Ras-GDP

Now attempting to coerce this statement into a single fact of the form aRb yields:

A correct translation of this is:

"Sos" "recruited to" "cell membrane" "implies" "Sos" "bound to" "Ras-GDP"

but in our concise notation this is a statement of the form:

aRbScTd

where a, b, c and d are "Sos", "cell membrane", "Sos" and "Ras-GDP" respectively.

and

R, S, and T are "recruited to", "implies" and "bound to" respectively.

Suddenly both the problem and the solution present themselves from prior art. We have a statement of the form:

aRb implies cTd

If we have a chain of facts of the form:

aRbScTd

there is a scope or binding of relationships that requires parentheses. Parentheses do not just enforce order of evaluation, they also provide correct grouping of relationships at all points along the way. Parentheses, with their encapsulating shape hint at the correct graph construction themselves. Correct parentheses for our example would be:

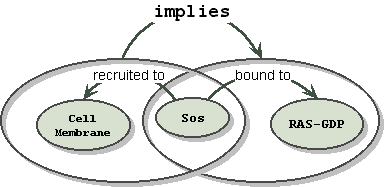
("Sos" "recruited to" "cell membrane") implies ("Sos" "bound to" "Ras-GDP")

These immediately suggest the idiom of a subgraph:

Which for the general case looks like:

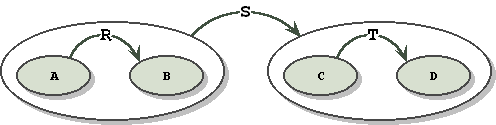
where A and C are the same in the Sos case.

Notice that the implication relationship S does not penetrate either of the two subgraphs. Each subgraph is a complete and intact fact. The implication relationship is over the complete and intact facts, not over entities that are part of the fact. In the general case however, penetration could occur, if an entity in the subgraph is referenced in a separate fact. Notice that defining the scope of relationships, using subgraphs as grouping operators, solves our problem, at the cost of added complexity.

In the Sos example above, the Sos node is a "common subexpression" appearing in both the first and second subgraphs. If we don't want to have multiple instances of Sos, the drawing looks like:

Multiple instances of Sos could require that all incoming arcs that are Sos specific have their own copy of incoming relationships, which would double the density of the arcs, increasing the "busy-ness" of the graph without adding to its readability.

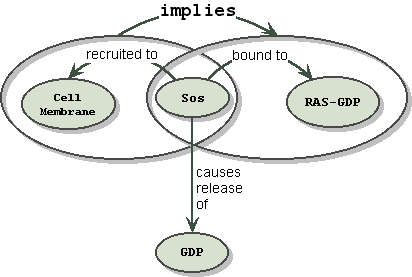
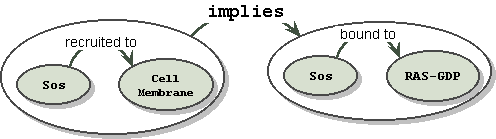
When an additional fact is added, that "Sos" "causes release of" "GDP", this arc is allowed to penetrate the envelop since it binds to the entity Sos, and not to the entire fact envelope. This piercing of the veil works for incoming as well as outgoing relationships. Notice that now, GDP, like Sos before, has been double booked, but we would leave this alone since it is considered primitive when in the complex of RAS-GDP. This serves the purpose of the knowledge map.

The purpose of knowledge maps is not the final communication of meaning, but the rapid discovery of cause and effect relationships in the living cell, as informational raw material. This raw material for the construction of pathways and ontologies must be efficiently extracted by data mining of existing literature. For this reason, when rendering speed and simplicity are more important, we can first define and then invoke a special relationship called "spanning implication.

Definition: spanning implication relationships are assumed to extend past the scope of the connected entities, and the reach of that scope is not stated. Repeating our example with this definition:

("Sos" "recruited to" "cell membrane") implies ("Sos" "bound to" "Ras-GDP")

is rewritten as:

"Sos" "recruited to" "cell membrane" "spanning implication" "Sos" "bound to" "Ras-GDP"

is rewritten as the three facts:
"Sos" "recruited to" "cell membrane"
"cell membrane" "spanning implication" "Sos"
"Sos" "bound to" "Ras-GDP"

The general form of spanning implication looks like this:

and is completely equivalent to the alternate forms:

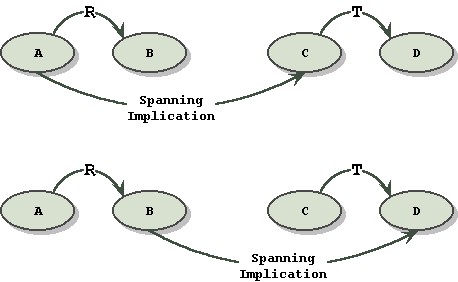
The purpose of spanning implication is to show that the facts connected by it are conditional on other facts in the local neighborhood, without unduly increasing the complexity of the graph.

It is conceivable for clarity that some translators would even render the passage as:

"Sos" "recruited to" "cell membrane"
"Sos" "bound to" "Ras-GDP"

which has the graph:

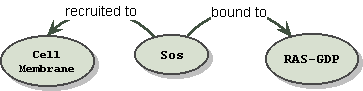
leaving more precise qualifications and descriptions for downstream ontologies and simulations. In this case we have dropped the notion of implication and predicate entirely on the assumption that a conditional fact, if ever true, is still a fact.

END