Comments On "Does Bell's Inequality Principle rule out local theories of quantum mechanics?"

In 1935 Albert Einstein and two colleagues, Boris Podolsky and Nathan Rosen (EPR) developed a thought experiment to
demonstrate what they felt was a lack of completeness in quantum mechanics. This so-called "EPR paradox" has led to much subsequent, and still on-going, research. This article is an introduction to EPR, Bell's inequality, and the real experiments
which have attempted to address the interesting issues raised by this discussion.

A well known example is position and momentum.
What about generalizing notion of locality in state space to include velocity?
Restatement is: What about velocity and momentum, ie. v and the product m v?
If you know v (allowed) you know m from m' = m₀/sqrt(1 - v²/c²).  Since you know m₀ and v, you know both, so
velocity and momentum are simultaneously observable.   Just wondered...

They imagined two physical systems that are allowed to interact initially so that they subsequently will be defined by a single Schrodinger wave equation (SWE). [For simplicity, imagine a simple physical realization of this idea - a neutral pion at rest in your lab, which decays into a pair of back-to-back photons. The pair of photons is described by a single two-particle wave function.] Once separated, the two systems [read: photons] are still described by the same SWE, and a measurement of one observable of the first system will determine the measurement of the corresponding observable of the second system.  [Example: The neutral pion is a scalar particle - it has zero angular momentum. So the two photons must speed off in opposite directions with opposite spin. If photon 1 is found to have spin up along the x-axis, then photon 2 must have spin down along the x-axis, since the total angular momentum of the final-state, two-photon, system must be the same as the angular momentum of the initial state, a single neutral pion. You know the spin of photon 2 even without measuring it.] Likewise, the measurement of another observable of the first system will determine the measurement of the corresponding observable of the second system, even though the systems are no longer physically linked in the traditional sense of local coupling.

Then there is the HUGE notion of representation.  A wave function is just a representation of an underlying phenomenon.  So is a particle.  In fact, both are just unrealizable abstractions that work approximately well in their domain of representation.

The article continues on.

How do we reconcile the fact that photon 2 "knows" that the x-spin of photon 1 has been measured, even though they are
separated by light-years of space and far too little time has passed for information to have travelled to it according to the
rules of Special Relativity? There are basically two choices.

Choice 1:
You can accept the postulates of QM as a fact of life, in spite of its seemingly uncomfortable coexistence with special relativity

Choice 2:
You can postulate that QM is not complete, that there was more information available for the description of the two-particle system at the time it was created, carried away by both photons, and that you just didn't know it because QM does not properly account for it.

 Choice 2 seems more plausible, because regardless of the speed of signal tranmission, there has to be some yet unexplored causal connection between the two events.

So, EPR postulated that the existence of hidden variables, some so-far unknown properties, of the systems should account
for the discrepancy. Their claim was that QM theory is incomplete; it does not completely describe the physical reality.
System II knows all about System I long before the scientist measures any of the observables, thereby supposedly
consigning the other noncommuting observables to obscurity.

I am with them, but just up to here.

Furthermore, they claimed that the hidden variables would be local.

This is where the opportunity opens up as of this writing (5/22/98)

No instantaneous action-at-a-distance is necessary in this picture, which postulates that each System has more variables than are accounted by QM.  Niels Bohr, one of the founders of QM, held the opposite view and defended a strict interpretation, the Copenhagen Interpretation, of QM.

In 1964 John S. Bell proposed a mechanism to test for the existence of these hidden variables, and he developed his
inequality principle as the basis for such a test. He showed that if his inequality was satisfied, then there could be no local hidden variable theory which accounted for it.

Use the example of two photons configured in the singlet state, consider this: After separation, each photon will have spin
values for each of the three axes of space, and each spin can have one of two values; call them up and down. Call the axes
A, B and C and call the spin in the A axis A+ if it is up in that axis, otherwise call it A-. Use similar definitions for the other two axes.

Note of an assumption: the notion of something spinning is a completely macromorphic view of the world.  It imposes a state space of a fixed size (6 values, A+, A-, B+, B-, C+, C-) onto an entity. (rifle left, rigle right, bowling top, bowling back, gyro clock, gyro counter)

Now perform the experiment. Measure the spin in one axis of one particle and the spin in another axis of the other photon. If EPR were correct, each photon will simultaneously have properties for spin in each of axes A, B and C.

Look at the statistics. Perform the measurements with a number of sets of photons. Use the symbol N(A+, B-) to designate
the words "the number of photons with A+ and B-." Similarly for N(A+, B+), N(B-, C+), etc. Also use the designation
N(A+, B-, C+) to mean "the number of photons with A+, B- and C+," and so on. It's easy to demonstrate that for a set of
photons

    (1)   N(A+, B-) = N(A+, B-, C+) + N(A+, B-, C-)

from a pure population count, similarly by extension and cyclic permutation:
 or (2) N(B+, C-) = N(A+, B+, C-) + N(A-, B+, C-)
    Statement (2)   N(A+, B+) = N(A+, B+, C+) + N(A+, B+-, C-)
or if you prefer the number of statements generated by expansion of:

    Statement (i,j)                 N(Ai, Bj) = N(Ai, Bj, C+) + N(Ai, Bj, C-)
of which there are 4 such statements
or if you prefer the number of statements generated by the further generalization:

    Statement W(i,j)          N(Ui,Vj) = N(Ui, Bj, V+) + N(Ui, Bj, V-)
where U, V, and W can be any of A, B, and C.
of which there are six such statements

there are also the corrollaries that:

                          N(A+) = N(A+, Bi, Cj)
and
                          N(U+) = N(U+, Vi, Wj)

because all of the (A+, B-, C+) and all of the (A+, B-, C-) photons are included in the designation (A+, B-), and nothing
else is included in N(A+, B-). You can make this claim if these measurements are connected to some real properties of the
photons.

Let n[A+, B+] be the designation for "the number of measurements of pairs of photons in which the first photon measured
A+, and the second photon measured B+." Use a similar designation for the other possible results. This is necessary because
this is all it is possible to measure. You can't measure both A and B of the same photon. Bell demonstrated that in an actual
experiment, if (1) is true (indicating real properties), then the following must be true:

    (2)    n[A+, B+] <= n[A+, C+] + n[B+, C-].

I have taken the liberty of visualizing the statement as follows:

Key: 

Then 

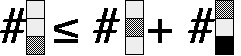
Additional inequality relations can be written by just making the appropriate permutations of the letters A, B and C and the two signs. This is Bell's inequality principle, and it is proved to be true if there are real (perhaps hidden) variables to account for the measurements.

At the time Bell's result first became known, the experimental record was reviewed to see if any known results provided
evidence against locality. None did. Thus an effort began to develop tests of Bell's inequality. A series of experiments was
conducted by Aspect ending with one in which polarizer angles were changed while the photons were `in flight'. This was
widely regarded at the time as being a reasonably conclusive experiment confirming the predictions of QM.

Three years later Franson published a paper showing that the timing constraints in this experiment were not adequate to
confirm that locality was violated. Aspect measured the time delays between detections of photon pairs. The critical time
delay is that between when a polarizer angle is changed and when this affects the statistics of detecting photon pairs. Aspect  estimated this time based on the speed of a photon and the distance between the polarizers and the detectors. Quantum mechanics does not allow making assumptions about where a particle is between detections. We cannot know when a particle traverses a polarizer unless we detect the particle at the polarizer.

Experimental tests of Bell's inequality are ongoing but none has yet fully addressed the issue raised by Franson. In addition there is an issue of detector efficiency. By postulating new laws of physics one can get the expected correlations without any nonlocal effects unless the detectors are close to 90% efficient. The importance of these issues is a matter of judgement.

The subject is alive theoretically as well. Eberhard and later Fine uncovered further subtleties in Bell's argument. Some
physicists argue that there are assumptions in derivations of Bell's inequality and that it may be possible to construct a local theory which does not respect those assumptions. The subject is not yet closed, and may yet provide more interesting
insights into the subtleties of quantum mechanics.

References

   1.A. Einstein, B. Podolsky, N. Rosen: "Can quantum-mechanical description of physical reality be considered
     complete?" Physical Review 41, 777 (15 May 1935). (The original EPR paper)
   2.D. Bohm: Quantum Theory, Dover, New York (1957). (Bohm discusses some of his ideas concerning hidden
     variables.)
   3.N. Herbert: Quantum Reality, Doubleday. (A very good popular treatment of EPR and related issues)
   4.M. Gardner: Science - Good, Bad and Bogus, Prometheus Books. (Martin Gardner gives a skeptics view of the
     fringe science associated with EPR.)
   5.J. Gribbin: In Search of Schrodinger's Cat, Bantam Books. (A popular treatment of EPR and the paradox of
     "Schrodinger's cat" that results from the Copenhagen interpretation)
   6.N. Bohr: "Can quantum-mechanical description of physical reality be considered complete?" Physical Review 48, 696
     (15 Oct 1935). (Niels Bohr's response to EPR)
   7.J. Bell: "On the Einstein Podolsky Rosen paradox" Physics 1 #3, 195 (1964).
   8.J. Bell: "On the problem of hidden variables in quantum mechanics" Reviews of Modern Physics 38 #3, 447 (July
     1966).
   9.D. Bohm, J. Bub: "A proposed solution of the measurement problem in quantum mechanics by a hidden variable
     theory" Reviews of Modern Physics 38 #3, 453 (July 1966).
  10.B. DeWitt: "Quantum mechanics and reality" Physics Today p. 30 (Sept 1970).
  11.J. Clauser, A. Shimony: "Bell's theorem: experimental tests and implications" Rep. Prog. Phys. 41, 1881 (1978).
  12.A. Aspect, Dalibard, Roger: "Experimental test of Bell's inequalities using time- varying analyzers" Physical Review
     Letters 49 #25, 1804 (20 Dec 1982).
  13.A. Aspect, P. Grangier, G. Roger: "Experimental realization of Einstein-Podolsky-Rosen-Bohm gedankenexperiment;
     a new violation of Bell's inequalities" Physical Review Letters 49 #2, 91 (12 July 1982).
  14.A. Robinson: "Loophole closed in quantum mechanics test" Science 219, 40 (7 Jan 1983).
  15.B. d'Espagnat: "The quantum theory and reality" Scientific American 241 #5 (November 1979).
  16."Bell's Theorem and Delayed Determinism", Franson, Physical Review D, pgs. 2529-2532, Vol. 31, No. 10, May
     1985.
  17."Bell's Theorem without Hidden Variables", P. H. Eberhard, Il Nuovo Cimento, 38 B 1, pgs. 75-80, (1977).
  18."Bell's Theorem and the Different Concepts of Locality", P. H. Eberhard, Il Nuovo Cimento 46 B, pgs. 392-419,
     (1978).