The Simply Supported Beam  
Distributed Load Problem
Van Warren
Warren Design Vision

Problem: A simply supported beam is subjected to a distributed load that varies linearly along its span. The expression for the distributed load is:

where and are constants.

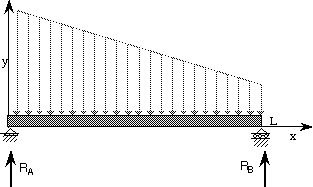
Determine the reactions at each of the supports, the deflection along the span, the slope at the endpoints, the shear and the bending moment.

Solution:
L = beam length
RA = the reaction at support A
RB = the reaction at support B
wm = slope of spanwise load function
wb = intercept of spanwise load function.
y(x) = deflection as a function of x.
V(x) = shear as a function of x.
M(x) = bending moment as a function of x.

We will solve the problem in two parts. First we sum forces and moments to deduce the values of the reactions at supports A and B. Then we will produce expressions to describe the deflection, shear and bending moments.

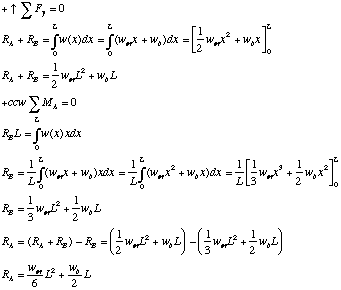
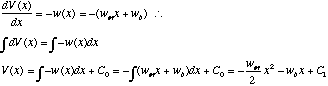
So now we have the reactions in terms of the load distribution and beam length. Now we need to compute the shear, bending moment, beam deflection and end slopes. We will begin with shear:

Now we need to plug in the boundary condition to find the value of C1:

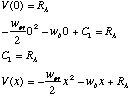
Which gives us a complete result for shear. Now we proceed with bending moment:

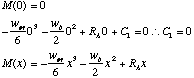
Which gives us a complete result for bending.
To compute spanwise deflection and slope we must refer to linear bending theory which (under the assumption of constant stiffness) gives us that:

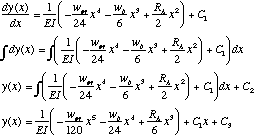
Having completed this integration we can now evaluate both remaining constants by inserting the boundary conditions:

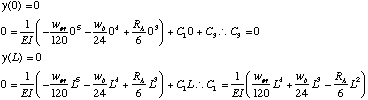
With this behind us we can generate complete expressions for the deflection and slope:

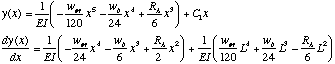
Our only remaining errand is to evaluate the slope expression at the endpoints:

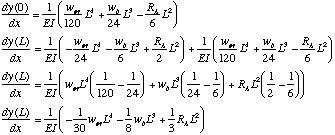
and to remember that end slopes are in radians.

Example Problem 1:

We first run a BeamCALCulator that only handles a uniform load:

Load Parameters

Load wm: 0; Slope of spanwise load function
Load wb: 10 lbs/in; Uniform Load
Length: 36 in;

Material Parameters

Material: Aluminum 6061 T-6
Elastic Modulus: 10,100,000 psi
Yield Strength: 35,000 psi (Tensile)
Density: 0.098 pci

Cross Sectional Parameters

Outer Width W: 1.00 inches
Inner Width w: 0.85 inches
Outer Height H: 1.00 inches
Inner Height h: 0.85 inches

Example Problem 2:

We then run a BeamCALCulator that handles a linearly varying load with the uniform load case and compare the results:

Load Parameters

Load wm: 0; Slope of spanwise load function
Load wb: 10 lbs/in; Uniform Load
Length: 36 in;

Material Parameters

Material: Aluminum 6061 T-6
Elastic Modulus: 10,100,000 psi
Yield Strength: 35,000 psi (Tensile)
Density: 0.098 pci

Cross Sectional Parameters

Outer Width W: 1.00 inches
Inner Width w: 0.85 inches
Outer Height H: 1.00 inches
Inner Height h: 0.85 inches

Example Problem 3:

We then run a BeamCALCulator that handles a linearly varying load with a tapered load case whose end support reactions are the same and compare the results:

Load Parameters

Load wm: -720/L2=.56 lbs/in2 Slope of spanwise load function
Load wb: 20 lbs/in; Uniform Load
Length: 36 in;

Material Parameters

Material: Aluminum 6061 T-6
Elastic Modulus: 10,100,000 psi
Yield Strength: 35,000 psi (Tensile)
Density: 0.098 pci

Cross Sectional Parameters

Outer Width W: 1.00 inches
Inner Width w: 0.85 inches
Outer Height H: 1.00 inches
Inner Height h: 0.85 inches