
my modest SL setup
Recent
News (2008)
![]() Purdue
Professor Sanctioned for Unsubstantiated Claims
Purdue
Professor Sanctioned for Unsubstantiated Claims
![]() Evidence
Bubbles Over in Support of Tabletop Fusion
Evidence
Bubbles Over in Support of Tabletop Fusion
![]() Science
Magazine Article - charging for this
after NPR announcement
Science
Magazine Article - charging for this
after NPR announcement
![]() Gaitan & Crum
@ UWash - 1988 - Early SL
Gaitan & Crum
@ UWash - 1988 - Early SL
![]() Joachim
Holzfuss @ Darmstadt - 1993 - SL Overview
Joachim
Holzfuss @ Darmstadt - 1993 - SL Overview
![]() Seth
Putterman @ UCLA - Feb. 1995 - SL Scientific American
Seth
Putterman @ UCLA - Feb. 1995 - SL Scientific American
![]() David
Knapp's Lawrence Livermorian introduction to SL.
David
Knapp's Lawrence Livermorian introduction to SL.
![]() American
Institute of Physics Overview
American
Institute of Physics Overview
![]() Aaron
Levinson @ UIUC - overview of SL
Aaron
Levinson @ UIUC - overview of SL
MIT
![]() Norman
Redington's Page
Norman
Redington's Page
![]() Micheal
Brenner
Micheal
Brenner
![]() MIT
Directed Search
MIT
Directed Search
Lawrence Livermore
National Laboratory
Advocates & Skeptics
Mathematical Investigations
Competing Explanations & Approaches
CASIMIR
![]() Casimir
Effect: Original by Philip Gibbs 24-January-1997
Casimir
Effect: Original by Philip Gibbs 24-January-1997
![]() The
Casimir effect - Interplays between theory and experiment.
The
Casimir effect - Interplays between theory and experiment.
![]() The
Casimir Force
The
Casimir Force
IMPINGING JET
![]() SL
bubbles collapse at 4x the speed of sound
SL
bubbles collapse at 4x the speed of sound
![]() Hopkins
scientist proposes new explanation for sonoluminescence in bubbles
Hopkins
scientist proposes new explanation for sonoluminescence in bubbles
SHAPE CONCERNS
![]() Spherical
symmetry deviation in SL bubble.
Spherical
symmetry deviation in SL bubble.
![]() SL
flashes can have a dipole shape
SL
flashes can have a dipole shape
QUANTUM PHYSICS APPROACHES
![]() Is
SL first observable manifestation of quantum vacuum radiation?
Is
SL first observable manifestation of quantum vacuum radiation?
![]() Eberlein,
C. "Sonoluminescence as Quantum Vacuum Radiation", Physical
Eberlein,
C. "Sonoluminescence as Quantum Vacuum Radiation", Physical
Review Letters, vol. 76, no. 20, 13 May 1996, pp. 3842-3845
OTHER APPROACHES
![]() Anne
Särkilahti's using the fourth-order Rosenbrock method
Anne
Särkilahti's using the fourth-order Rosenbrock method
![]() Van
Warren @ WDV - Jan 10, 1996 - Active Waveform Control
Van
Warren @ WDV - Jan 10, 1996 - Active Waveform Control
![]() Willie
Moss @ LLNL - March 29, 1996 - pressure spiking D20
Willie
Moss @ LLNL - March 29, 1996 - pressure spiking D20
![]() Keshishiam & Maybrun
@ UCLA - June 1996 - SL In H202
Keshishiam & Maybrun
@ UCLA - June 1996 - SL In H202
![]() Gary
Williams @ UCLA - home page - SL in liquid ethanol @ -115 C
Gary
Williams @ UCLA - home page - SL in liquid ethanol @ -115 C
![]() M.J.
Moran et. al @ LLNL - showing 12 picosecond pulse duration
M.J.
Moran et. al @ LLNL - showing 12 picosecond pulse duration
![]() Thomas
Matula - April 1996 - The Effects of Micro-Gravity
Thomas
Matula - April 1996 - The Effects of Micro-Gravity
![]() John
Parker: SL from ethane, and a good hypertext bibliography
John
Parker: SL from ethane, and a good hypertext bibliography
![]() University
of Manchester Institute of Science and Technology
University
of Manchester Institute of Science and Technology
![]() College
of William & Mary Physics Department Colloquia
College
of William & Mary Physics Department Colloquia
![]() 19th
International Symposium on Rarefied Gas Dynamics
19th
International Symposium on Rarefied Gas Dynamics
![]() NONLINEAR
DYNAMICS DAYS ARIZONA, Symposium
NONLINEAR
DYNAMICS DAYS ARIZONA, Symposium
![]() Third
Workshop on Quantum Field Theory
Third
Workshop on Quantum Field Theory
Technical Notes Candidate Fusion Reactions For The most important fusion reactions are: 1. D + T -> He-4 + n +
17.588 MeV |
|
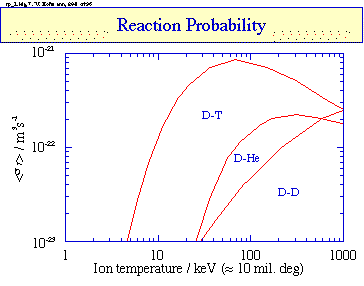 |
At
the temperatures found in fission, reaction 1 has a rate
100 times faster than the next fastest candidate (reactions 2 and
3 combined), which are in turn 10 times faster than reaction 4.
The rates of reactions 1 - 4 all increase rapidly (exponentially)
with temperature, but not in the same proportion. At the higher
temperatures achievable by fusion, reaction 4 exceeds the combined
rate of reactions 2 and 3. Other reactions also occur between
the isotopes listed here, but the reactions rates are too low to
be important. Some additional important facts about these reactions: |
| To
produce fusion we choose a reaction with the highest probability
of occurrence: This easiest reaction is the one between deuterium (D) and tritium (T). To manufacture tritium, half-life 12.4 years, one bombards lithium with neutrons. The production of tritium can also be carried out in fission provided that each event that produces one spare neutron, releases 180 MeV of energy. If the spare neutron is captured by Li-6, producing one atom of tritium, which then fuses, we get a total energy production of 22.4 MeV. See:http://www.ipp.mpg.de/w7as/jvh/jvh_html/fusion/fusion2.html. The neutron produced in reaction 1 is extremely energetic, it carries away 14.06 MeV of the reaction energy, the alpha particle (He-4 nucleus) only 3.52 MeV. The neutron produced in reaction 2 has an energy of only 2.45 MeV (similar to the faster fission neutrons), with the He-3 carrying 0.82 MeV. The division of energy in reaction 3 is 1.01 MeV for the triton, and 3.03 MeV for the proton. The two D+D reactions are equally likely and each will occur half the time. In reaction 4 the alpha particle carries off 3.67 MeV, the proton 14.67 MeV. |
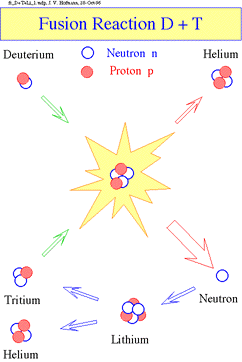 |
|
Reactions 5 and 6 are not thermonuclear reactions, strictly speaking. They are neutronic reactions, like fission, and do not require heat or pressure, just neutrons in the correct energy range. This distinction is usually ignored in the literature . The Li-6 + n reaction requires neutrons with energies is the low MeV range or below. The Li-7 + n reaction is only significant when the energies are above 4 MeV. For fusion to occur, one must simultaneously maintain the pressure, temperature and particle density at a sufficient level. Some remarks on this are: |
|
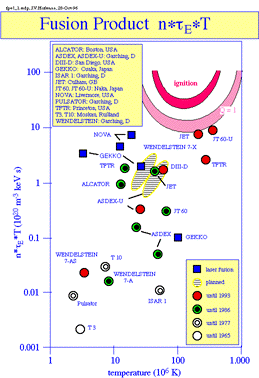 |
1)
For the ignition and sustained burn of a plasma the fusion
product n*tau*T of the ion density, the energy confinement
time and the ion temperature has to exceed a value of 50*1020
keV/m3. This has to be realized by ion densities of the order
of 2-3*1019 m-3, energy confinement times of the order of 1-2
seconds and ion temperatures of the order of 20 keV (about
200 Million degrees). While
all these three individual values have been exceeded in present
experiments the combined product has not been reached, yet. Since
the last 30 years the world wide effort to reach this value has
resulted in improvements of the order of 10000, but there is still
a factor of about 10 missing.
2) The first type of generator to be invented relies
on the fact that one of the neutrons in beryllium-9 is easily knocked
loose. Occasionally if it is struck by an alpha particle, like
those produced by some produced by some radioactive isotopes, a
neutron will be released as a result of the collision:
Be-9 + He-4 -> Be-8 + n
+ He-4
This happens in only 0.008% of collisions, so a
strong alpha emitter (like polonium-210) is required to achieve
the neutron flux needed. Ref.
|
|
It
is desirable to use fuels that are cheaper, and more stable
than tritium. Deuterium, the sole fuel in reactions 2 and 3,
is relatively cheap (especially considering its enormous energy
content) and is completely stable. Pure deuterium has been
used in at least one fusion weapon test - Ivy Mike, arguably
the first true fusion explosion in history (1 November 1952).
Unfortunately deuterium, like all elemental hydrogen, is difficult
to store. It must either be highly compressed, or liquefied
at extremely low temperatures. This problem can be overcome
by combining the deuterium chemically with lithium to form
lithium deuteride, a stable solid. An additional benefit is
that through reactions 5 and 6, the lithium can itself participate
in the fusion reaction.
To make use of these fuels, the slower reaction
rates must be offset by compressing them to densities hundreds
or thousands of times greater than those of normal conditions.
At any given temperature the reaction rate goes up with the square
of the density, a thousand-fold compression gives a million-fold
reaction rate increase.
The work required to compress a gas is proportional
to its temperature (at these pressures the physical strength of
materials is negligible, and everything can be considered a gas).
To minimize the work required for compression, or alternatively
to achieve maximum compression for a given amount of work, it is
important to keep the fusion fuel from getting hot until after
the desired density is reached.
The fuel in the fission capsule consists of lithium
deuteride that may be enriched in the Li-6 isotope (which makes
up 7.5% of natural lithium). Natural lithium has been used but
modern light weight designs seem to use lithium enriched in Li-6.
There is some tritium generated by the fission neutrons, but as
noted above the contribution to yield is insignificant. Far more
tritium is produced by the D+D reactions, either directly by reaction
3, or by reaction 5 via the neutrons produced in reaction 2.
Since the D+T reaction rate is so high, and there
is large excess of deuterium, the tritium is consumed almost as
fast it is produced. The 14.1 MeV neutrons can also produce large
amounts of tritium from Li-7 through reaction 6.
A large part of the fusion fuel can be burned before
expansion quenches the reaction by reducing the density, which
takes some 20-40 nanoseconds. The power output of a fusion capsule
is noteworthy. The largest yield ever recorded had a yield of 50
megatons almost all produced by its final fusion stage. Since 50
megatons is 2.1x10^17 joules, the power produced during the burn
was around 5.3x10^24 watts. This is more than one percent of the
entire power output of the Sun (4.3x10^26 watts)!! The peak output
was possibly even greater. Definitely the hot set up for
solar system exploration.
|
|
|
Noble Gas Notes Molecular or polyatomic gases, ones in which the particles are molecules of two or more atoms, can absorb energy through rotation and vibration. Such gases are not monatomic, but they are still ideal. Under some conditions gases can absorb energy internally by other processes, like ionization, which violate ideal gas behavior. When conditions are such that attractive forces become significant (near liquid or solid condensation points) the ideal gas law also breaks down. Perfect monatomic gases are of special interest to us here, not only because they are particularly simple to analyze, but because under many extreme physical regimes all matter tends to behave like a perfect monatomic gas (kinetic energy dominates other forms of energy present). From:
http://www.phys.uni.torun.pl/~jkob/physnews/node127.html -- excerpted from http://www.onestep.com/milnet and other links where noted |
|
Symposium
on Sonoluminescence Program of 9/2/97 |
|
8:40
- 9:20 S. Putterman "Defining the Unknowns of SL" |
Session II 10:20
- 11:00 H. Kuttruff "Bubble Dynamics and SL in Multi-Bubble Cavitation
Fields" |
Session III 1:30
- 2:10 D. Lohse "SL Air Bubbles Rectify Argon" |
Session IV 3:15
- 4:15 Open Forum on the Future of Sonoluminescence |
Saturday, September 13, 1997 Session V 8:30
- 9:10 K. Suslick "Multi-Bubble Sonoluminescence" |
Session VI 10:15
- 10:55 R. Laughlin "Theory of Ultrafast Temperature Measurement
of SL" |
Session VII 1:30
- 2:10 T. Matula "Sonoluminescence Experiments" |
Session VIII 3:15
- 3:55 H. Maris "Nucleation of Bubbles in Superfluid helium: Quantum
Tunneling and Exploding Electrons" |
