Cell Born Computing

Van Warren

12/99

Introduction

We don't know what the possible outcomes of this line of experimentation, but it is the process of directed searching and inquiry that produce new opportunities.

Potential uses

1) nano level cell instrumentation

cell is instrumented to disclose information as part of its housekeeping functions.

2) combinatorial problem solving

as in combinatorial chemistry, large solution spaces are searched in parallel by many cellular processors working concurrently

3) biological interface to computing systems

currently, all computer input takes place through the hands and

all computer output takes place through the eyes and ears.

biocompatible implants, such as artificial retinas are already moving in this direction, but are still somewhat clumsy and low in resolution and bandwidth

Practical examples

classic computer science problems

examine plausible biological embeddings of these problems

execute them to solution and ask

• what did we learn
• what are the implications

Part One

representing information in cellular systems

simple arithmetic, predicates, comparison, threads of execution

sorting and searching

Representing Information in Cellular Systems

There are two kinds of computational entity that we can represent at any level, in any system, they are the dual forms:

• data (which can be program) and
• program (which can be data)

At the cellular level, patterns of information are represented as:

• the number of cells,
• types of cells,
• cells expressing a certain property
  for example a luminescent reporter gene,
• as a life or death state,
• biological objects themselves.

At the subcelluar level, patterns of information can be represented as:

• proteins sequences
• folding conformations
• amounts of substances
• combination of components
  (example monomers, versus dimers versus multimers)
• separation of components
• the number of cellular compartments
• the number of compartments that are performing a specific activity
• the number of compartments in a specific state

Since we would ultimately like these methods to be human compatible and therapeutic, for our initial investigations we will set the following goals.

Non destructive write in.

• No damage to cell during problem set up.

Non destructive execution.

• No damage to cell during execution of the program.

Non destructive read out.

• Readout of the solution without damage to the cell.

Initial Choices

We would like to represent information the way the cells does, as DNA sequences.

We will take for our first problem the problem of representing, sorting and searching a list of names.

Representing a list of names.

BNF for Ideal LALR Grammar:

list: nameUnit OR

nameUnit list

nameUnit: intron name intron

name: sixtyFourBases

intron: weDecideBasedOnNonDestructiveDoctrine

concurrent versus concatenated representations

concatenate, solve, concatenate

the reading problem

results as sequences

results as proteins

results as macro level objects

References:

http://www.hks.net/~cactus/doc/science/molecule_comp.html

http://www.cs.sandia.gov/jcb/v6/n1/v6n1art4.html

Experiment 1: Certain Preliminaries

The difficult part of the sorting and searching problem described above is designing a sorting algorithm that works in vivo. The major histocompatibility complex (MHC) performs exon shuffling, but shuffling is the opposite of sorting. We desire to create the minimal sorting operations of selection and successive positional exchange. One possible mechanism for accomplishing this is RNA intron self-splicing. Prior to embarking on this ambitious goal, it is useful to examine equilibrium structures of our name list. This was performed in the first of a series of numerical experiments outlined below.

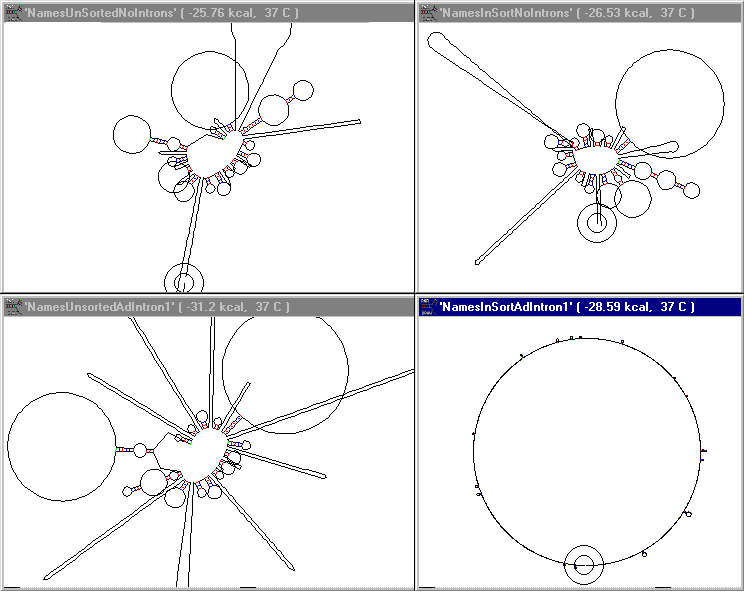
The list of 10 person names, each consisting of 16 ASCII characters was translated into an arbitrary 64 nucleotide mapping. These names are taken directly from the name representation section computed above. These are shown in their RNA secondary structures as computed by RNADraw1.06 below. The results are shown in the 2 x 2 array of images below. Proceeding from left to right shows the effect of sorting only. Proceeding from top to bottom shows the effect of adding an intron only. The intron in this naive case is a 64 nucleotide intron of the form GU-AAA...-AG. No pyrimidine rich section preceded the AG. The result is that adding introns to the unsorted list opened up but failed to geometrically delimit the final structure. Similarly presorting the list suffered from the same limitation. When presorting and adding introns occur simultaneously, the result is the significant change in secondary structure shown in the lower right frame. (widen your browser to see this...)

The titles on the images indicate conditions.
Zooming in on the same content we can see more clearly the fine structure of the RNA self-annealing.

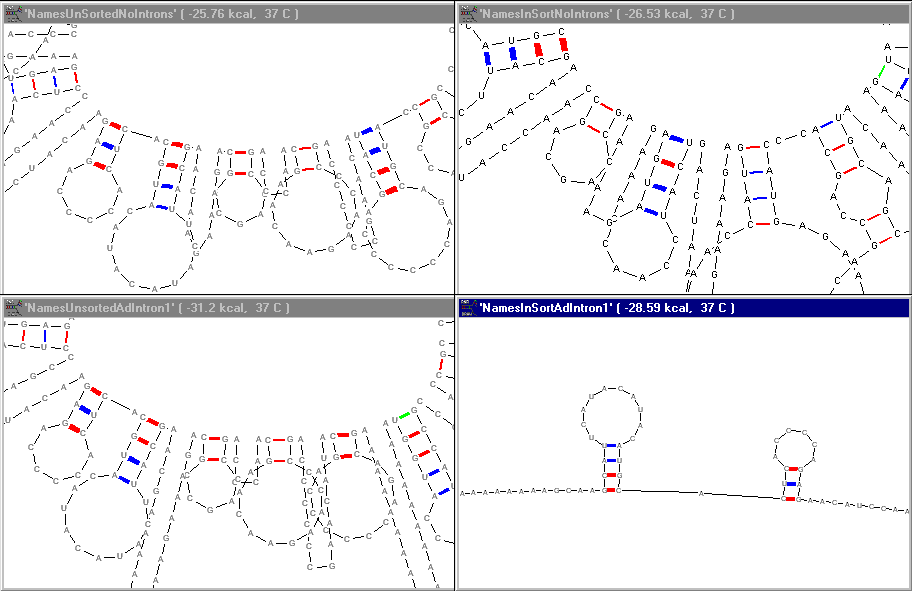
The next step will be to design introns which delineate the names in a more accessible fashion for selection and exchange.

The critical sections of a sort are:

1. selection
2. comparison
3. exchange

Before we figure out how to encode these three primitive operations actions, lets improve our understanding of RNA self-annealing.

Experiment 2: Random RNA's

We examine the annealing patterns of 9 randomly generated RNA's, each consisting of 64 bases. Each of these patterns is unique and forms a pictograph containing 64 * 4 = 256 bits of information. There 3.4 * 10^38 of these symbols. A very large vocabulary. Six bases would give the ability to represent 1024 possible symbols. We might want to restrict certain combinations of symbols as forbidden if they had undesireable preexisting meanings to biological systems. We might want to represent symbols using multiples of three bases, since triplets form codons in genes. We might want to represent symbols using combinations of the three stop codes UAA, UAG, UGA, so that we could guarantee that no proteins would be generated.

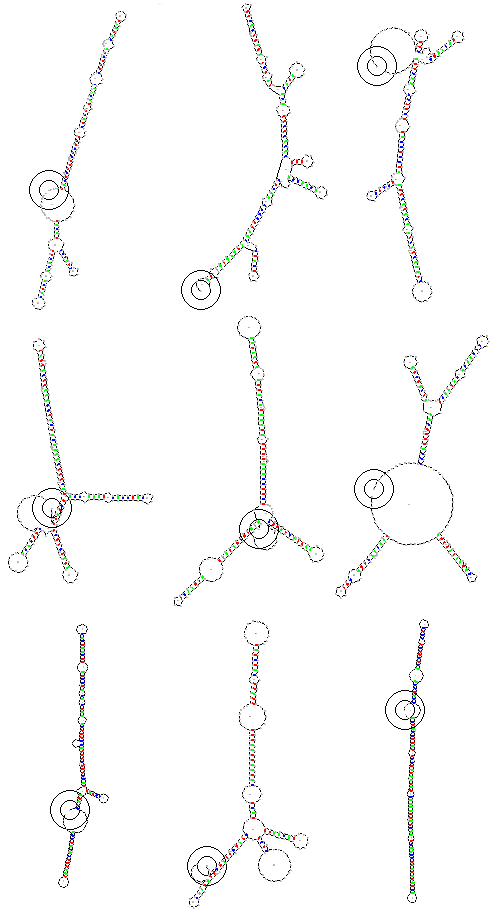
- lvw99

We might choose to have the cellular machinery serve us at one point, and then convert to a representation that would not interfere with a follow-on computation. This could be done with permutations of stop codes, which would be transcribed by RNA polymerase, but not translated by ribosomes creating proteins that would risk damaging the cell. This is consistent with our non damaging doctrine stated above.

By using only stop codes, we have lost some of the economy of a terse representation of information, but we have greatly gained in our ability to express safe computation. We are now ready to design a refined grammar. With six places in a base 3 system (from the 3 stop codes representing 0, 1, and 2 respectively) we can represent 243 characters, which is the entire ASCII character set plus change. This will require six places consisting of 18 actual bases. To represent a 16 letter name will require 288 bases. Attempts to shorten this are unproductive since five places can only represent 81 characters but still requires 240 bases to represent a 16 letter name. A simulation of these choices is attached, use the Excel sheet labeled Combinations. In the next section this method will be applied to the name list and the alphabet of RNA's will be produced.